Question 1060844: I would like to know what formula can I use to solve the nth term of this particular sequence. 5, 12, 25, 50, 93
Found 2 solutions by Edwin McCravy, rothauserc:
Answer by Edwin McCravy(20056)   (Show Source):
You can put this solution on YOUR website!
First we use a difference table to find out what degree of
polynomial general solution assume:
We list the terms in a column, subtract each number from the
number just beneath it, and write the difference out beside
the number. Then we do the same thing with the new column.
W continue making new columns until we come to a column which
only contains only one number, or the same number over and over.
5 7 6 6
12 13 12 6
25 25 18
50 43
93
Since it took 3 columns past the one with the original sequence
to find one with only one number, 6, we know that the general
formula must have degree 3, and we'll need the first 3+1 or 4
terms of the sequence
So we assume
  
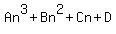We substitute n=1,2,3,4
  
  
  
 
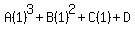
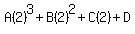
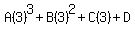
Simplifying we have the system of equations:
Subtract 1st equation from 2nd equation.
Subtract 2nd equation from 3rd equation.
Subtract 3rd equation from 4th equation.
Get this system:
Subtract 1st equation from 2nd equation.
Subtract 2nd equation from 3rd equation.
Get this system:
Subtract 1st equation from 2nd equation.
Get this equation:
Solving that we get
Substitute A=1 in
Substitute A=1 and B=-3 in
Substitute A=1, B=-3, and C=9 in
The general formula:
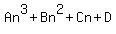becomes
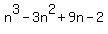The sequence goes:
5, 12, 25, 50, 93, 160, 257, 390, 565, 788, 1065, 1402, 1805,...
Edwin
Answer by rothauserc(4718)  (Show Source):
You can put this solution on YOUR website! This is a cubic sequence, the general form is
:
an^3 +bn^2 +cn +d = 0
:
the method of differences confirms a common difference of 6 at the 3rd level
:
using the first four terms, we get the following points
:
(1,5), (2,12), (3,25), (4,50)
:
We have four equations in 4 unknowns
:
a +b +c +d = 5
8a +4b +2c +d = 12
27a +9b +3c +d = 25
64a +16b +4c +d = 50
:
use Cramer's rule calculator
:
a = 1, b = -3, c = 9, d = -2
:
***********************
x(n) = n^3 -3n^2 +9n -2
***********************
:
|
|
|
