|
Question 1057049: A small combination lock on a suitcase has 5 wheels, each labeled with the 10 digits 0 to 9. how many 5-digit combinations are possible if digits can be repeated? (hint: the word combination is a misnomer. Lock combinations are not mathematical combinations because the arrangement of the numbers is important.) Please help, this is confusing
Answer by ikleyn(52788)   (Show Source):
You can put this solution on YOUR website! .
A small combination lock on a suitcase has 5 wheels, each labeled with the 10 digits 0 to 9. how many 5-digit combinations
are possible if digits can be repeated?
(hint: the word combination is a misnomer. Lock combinations are not mathematical combinations
because the arrangement of the numbers is important.) Please help, this is confusing
~~~~~~~~~~~~~~~~~~~~~~~~~~~
10 options for the first (leftmost) wheel. (From 0 to 9, no exclusions).
10 options for the second wheel.
10 options for the 3-rd wheel.
10 options for the 4-rd wheel.
10 options for the 5-rd wheel.
10*10*10*10*10 = 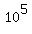 = 100000.
Repeating is allowed, according to the condition.
There are no any restrictions, according to the condition.
The words "the word combination is a misnomer" mean that zero is allowed as the first digit, if I correctly understand this term.
Wikipedia says:
A misnomer is a word or term that suggests a meaning that is known to be wrong. Misnomers often arise because the thing received
its name long before its true nature was known, or because the nature of an earlier form is no longer the norm.
A misnomer may also be simply a word that is used incorrectly or misleadingly.[1]
"Misnomer" does not mean "misunderstanding" or "popular misconception",[1] and many misnomers remain in legitimate use
(that is, being a misnomer does not always make a name incorrect).
The other popular source says
1. a misapplied or inappropriate name or designation.
2. an error in naming a person or thing.
Not very meaningful explanations for me.
----------------------------------------
O-o-o!!! I got the meaning of the hint.
They want to say that their word "combination" is NOT the term from Combinatorics.
The word "combination" in their context is simply "the word comprising of digits".
OK, I understand it exactly in this sense/meaning.
By the way, on Combinations and Permutations see the lessons
- Introduction to Permutations
- PROOF of the formula on the number of Permutations
- Problems on Permutations
- Introduction to Combinations
- PROOF of the formula on the number of Combinations
- Problems on Combinations
- OVERVIEW of lessons on Permutations and Combinations
in this site.
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Combinatorics: Combinations and permutations".
|
|
|
| |
