SOLUTION: Find a and b if {{{sum( ak+b, k=1, n ) = 8n^2+11n}}}, given that {{{sum( k, k=1, n ) = (n(n+1))/2}}}

Algebra ->  Sequences-and-series -> SOLUTION: Find a and b if {{{sum( ak+b, k=1, n ) = 8n^2+11n}}}, given that {{{sum( k, k=1, n ) = (n(n+1))/2}}}      Log On


   

Question 1051855: Find a and b if sum%28+ak%2Bb%2C+k=1%2C+n+%29+=+8n%5E2%2B11n, given that sum%28+k%2C+k=1%2C+n+%29+=+%28n%28n%2B1%29%29%2F2
Found 2 solutions by Edwin McCravy, Bakr.R:
Answer by Edwin McCravy(20056) About Me  (Show Source):
You can put this solution on YOUR website!
Find a and b if sum%28+ak%2Bb%2C+k=1%2C+n+%29+=+8n%5E2%2B11n, given that sum%28+k%2C+k=1%2C+n+%29+=+%28n%28n%2B1%29%29%2F2
The easy way is to substitute n=1 and n=2, and not even bother
with sum%28+k%2C+k=1%2C+n+%29+=+%28n%28n%2B1%29%29%2F2

-----------------------------------------

Substituting n=1:

sum%28+ak%2Bb%2C+k=1%2C+1+%29+=+a%281%29%2Bb=a%2Bb=8%281%29%5E2%2B11%281%29=8%2B11=19

So a%2Bb=19

Substituting n=2



So 3a%2B2b=54

Solve the system:

system%28a%2Bb=19%2C3a%2B2b=54%29

by substitution or elimination

Get a=16, b=3 

sum%28+16k%2B3%2C+k=1%2C+n+%29+=+8n%5E2%2B11n

Edwin

Answer by Bakr.R(8) About Me  (Show Source):
You can put this solution on YOUR website!
Thank you Edwin, that was actually extremely helpful and a unique method, it wasn't how I would tackle the problem, but the question did ask a series of questions prior (in my maths textbook) to force me to use the equation sum%28+k%2C+k=1%2C+n+%29+=+%28n%28n%2B1%29%29%2F2 to find the answer (with the word "Hence"), so although your method works efficiently (and far more easily), a specific method was requested, and for those seeking that particular method, (I found during this question was being solved) here's how it was done.
sum%28+ak%2Bb%2C+k=1%2C+n+%29+=+8n%5E2%2B11n
With added coefficients, we can separate the terms each with its own sum, we reach:
sum%28+ak%2C+k=1%2C+n+%29+%2Bsum%28+b%2C+k=1%2C+n+%29+
Since we earlier found out sum%28+k%2C+k=1%2C+n+%29+=+%28n%28n%2B1%29%29%2F2
We may deduce that (with substitution)
a%2An%28n%2B1%29%2F2%2Bsum%28+b%2C+k=1%2C+n+%29+
and with coefficient b being the only term,
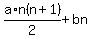a%2An%28n%2B1%29%2F2%2Bbn+ (since b is the only term and is a constant)
We expand terms
%28an%5E2%2Ban%29%2F2%2Bbn+=+8n%5E2%2B11n
We now follow a method of comparing coefficiants marked by the same variable, having each coefficient match its opposing equal value.
By splitting fractions to factorize to one variable of each, we have
an%5E2%2F2%2Ban%2F2%2Bbn+=+8n%5E2%2B11n
an%5E2%2F2%2Bn%28a%2F2%2Bb%29=+8n%5E2%2B11n
And so
an%5E2%2F2=8n%5E2
a%2F2=8
a=16
And moving to the second comparison,
n%28a%2F2%2Bb%29=11n We may substitute a
n%2816%2F2%2Bb%29=11n
8%2Bb=11
b=3
And with that relation we find a=16, b=3