Question 1046020: This is a question my teacher assigned if we want to do, it is extra, but I would like to learn more and this is a great problem. I cannot understand it no matter how hard I try. Please explain fully and how you got your answer.
For any positive integer, find the sum of the squares of its digits. If the result is 1, you’re done. Otherwise, find the sum of the squares of the digits of the result. Continue this process until the result is 1, in which case we call the original integer a happy number, or until there is a repeated result, which leads to an endless loop, in which case we call the original integer an unhappy number. For example, consider 13 and 85.
13 is a happy number since
12 + 32 = 1 + 9 = 10,
12 + 02 = 1 + 0 = 1.
85 is an unhappy number since
82 + 52 = 64 + 25 = 89,
82 + 92 = 64 + 81 = 145,
12 + 42 + 52 = 1 + 16 + 25 = 42,
42 + 22 = 16 + 4 = 20,
22 + 02 = 4, 42 = 16,
12 + 62 = 1 + 36 = 37,
32 + 72 = 9 + 49 = 58,
52 + 82 = 25 + 64 = 89, which is a repeated result.
What is the least unhappy number?
What is the least prime number that is a happy number?
What is the least integer greater than 1 that, when multiplied by any happy number, yields another happy number?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Squares end in 0, 1, 4, 5, 6, or 9.
To add up to 1 (or 10, or 100), only a few combinations work.
For a 2-digit numbers, you need to pair
0 with 1,
or 1 with 3, or
6 with 8.
Obviously  is a happy number, and so are is a happy number, and so are  , and , and  . .
Other happy numbers are
 , , 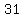 , , 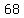 and and 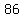 . .
The least unhappy number is  . .








2^2+0^2=4}}} and we went full loop back to  . .
That also tells us that as soon as we found a number, or a sum of squares that is
 , or , or  , or , or  , or , or  , or , or 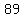 , or , or 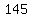 , or , or  , or , or  , ,
we know we have entered the loop above,
meaning that the original number is an unhappy number,
and so are all the other intermediate results.
Numbers with the same digits in a different order, are also unhappy,
because they will yield the same sum of squares.
The least prime that is a happy number is obviously not  . .
It is not  either, because either, because



 and and 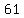 is as unhappy as is as unhappy as  , ,
bringing us into the same -->37-->58-->89--->145... unhappy loop we found for 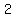 , is also unhappy: , is also unhappy:


 , and , and 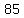 , as unhappy as , as unhappy as  brings us back into the brings us back into the
--->89--->145 ... loop we knew from  . .
The next prime is happy number  : :


 , and as , and as
 is happy, making is happy, making
 , ,  is the least happy prime number.From the sums above,m we see that is the least happy prime number.From the sums above,m we see that 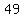 and and  are also happy numbers. are also happy numbers.
Obviously  is a number greater than is a number greater than  , ,
than when multiplied by any happy number gives a product with the same digits as the original number plus a zero added at the end,
so the product is also a happy number.
If there were a smaller factor whose products times a all happy numbers were happy, it would be a happy single digit number itself (as a product time happy  . .
However, all digits other than  and and  are unhappy, and while are unhappy, and while  is happy is happy  is not: is not:

 , and we knew that , and we knew that  is unhappy from testing is unhappy from testing  . .
So, I think the least nteger greater than 1 that, when multiplied by any happy number, yields another happy number is  . .
|
|
|