.
Let me reformulate the problem in this way:
x and y are real numbers such that |x| < 1 and |y|< 1.
Find the infinite sum 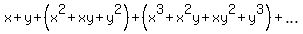
Solution
Let "S" be the infinite sum
S = 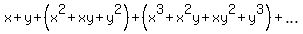 .
Multiply S by (x-y). Then
S =
.
Multiply S by (x-y). Then
S =  .
Now notice that
.
Now notice that
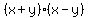 =
=  , (1)
, (1)
 =
= 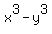 , (2)
, (2)
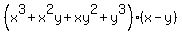 =
= 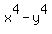 (3) (make yourself this calc . . . )
And so on . . .
So, I suppose (and I am almost sure) that each parenthesed term in the original sum, multiplied by (x-y) will give
(3) (make yourself this calc . . . )
And so on . . .
So, I suppose (and I am almost sure) that each parenthesed term in the original sum, multiplied by (x-y) will give 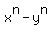 . (4)
//"The margins of this page are too narrow . . . "
Thus we have
S*(x-y) =
. (4)
//"The margins of this page are too narrow . . . "
Thus we have
S*(x-y) = 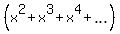 -
- 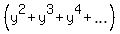 = (5)
Now apply the formula for the infinite sum of a geometric progression
=
= (5)
Now apply the formula for the infinite sum of a geometric progression
= 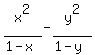 .
Simplify it and then cancel the factor (x-y) in both sides.
Finally, you will get
S =
.
Simplify it and then cancel the factor (x-y) in both sides.
Finally, you will get
S = 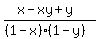 = 1 -
= 1 - 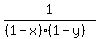 .
Again, the key is the idea with the formulas (1), (2), (3), (4), (5).
Answer. S =
.
Again, the key is the idea with the formulas (1), (2), (3), (4), (5).
Answer. S = 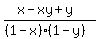 = 1 -
= 1 - 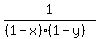 .
.