SOLUTION: Find the sum of the first n positive even integer Thank you in advance

2 + 4 + 6 + . . . 2n = 2*(1 + 2 + 3 + . . . + n).     (1)

The sum (1 + 2 + 3 + . . . +n) is very well known. 

It is the sum of the first "n" positive integers.

It is also the sum of "n" terms of an arithmetic progression with the first term 1 and the common difference 1.

This sum is equal to .

See, for example, the lessons 

    - Arithmetic progressions

    - The proofs of the formulas for arithmetic progressions 

    - Problems on arithmetic progressions  

in this site.

So, your sum (1) is equal to n*(n+1).

Let us check the first sums , , :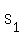

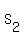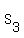n=1: 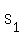  = 2.                     n*(n+1) = 1*2 = 2.

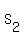n=2:   = 2 + 4 = 6.             n*(n+1) = 2*3 = 6.

n=3: 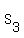  = 2 + 4 + 6 = 12.        n*(n+1) = 3*4 = 12.