What do you want to do with it?
I'll do what I can:
SUM = 1 - 4/5 - 3/5 - 8/17 - 5/13 - ...????
SUM = 2/2 - 4/5 - 6/10 - 8/17 - 10/26 - ...????
The sequence of absolute value of numerators is 2,4,6,8,10
The sequence of absolute value of denominators is 2,5,10,17,26
2,4,6,8,10 has general term 2n
1,5,10,17,26 has general term n2+1
The general term would be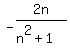 
except for the first
term being positive instead of negative, so we write the first term as
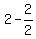SUM = 2 - 2/2 - 4/5 - 6/10 - 8/17 - 10/26 - ...????
So it could be written this way:
SUM = 
The next term after -10/26 (or -5/13) would be 
It can't be summed to infinity because it diverges when compared
to the harmonic p-series S(1/n).
Edwin
