Question 1028877: Find three number of G.P whose sum is 19 and product is 216
Found 2 solutions by mananth, ikleyn:
Answer by mananth(16946)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let the numbers be a/r, a,ar
a/r + a +r =19
a/r*a*ar=219
a^3= 216
a=6
a+ar+ar^2 = 19r
6+6r+6r^2=19r
6r^2-13r+6 =0
6r^2-9r-4r+6=0
3r(2r-3)-2(2r-3)=0
(2r-3)(3r-2)=0
r=3/2 OR r=2/3
plug a & r
when r=3/2
a/r = 6/(3/2) =4
a=6
ar = 9
4,6,9
OR r=2/3
a/r = 6/(2/3) =9
a= 6
ar = 4
9,6,4
Answer by ikleyn(52788)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find three number of G.P whose sum is 19 and product is 216
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Answer. 1) a = 9, r =  , and the progression is {9, 6, 4}; 2) a = 4, r = , and the progression is {9, 6, 4}; 2) a = 4, r =  , and the progression is {4, 6, 9}. , and the progression is {4, 6, 9}.
Solution
Let "a" be the first term of the GP, and "r" be the common ratio.
Then the three terms of the GP are  , , 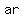 and and 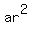 .
From the condition, we have these two equations .
From the condition, we have these two equations
 = =  , (1) , (1)
 = = 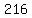 . (2)
From (2), you have . (2)
From (2), you have
 = = 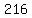 , hence, , hence, 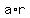 = = 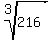 = 6. (3)
(I consider here only real solutions and do not consider complex values).
Based on (3), substitute 6 into (1) instead of the second addend. You will get = 6. (3)
(I consider here only real solutions and do not consider complex values).
Based on (3), substitute 6 into (1) instead of the second addend. You will get
 = =  , or , or
 = =  = =  . (4)
Now, from (3) express r = . (4)
Now, from (3) express r =  and substitute it into (4). You will get and substitute it into (4). You will get
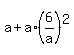 = =  , or , or
 = =  . (5)
Multiply both sides of (5) by a to red off the denominator. You will get . (5)
Multiply both sides of (5) by a to red off the denominator. You will get
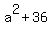 = =  , or , or 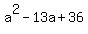 = =  . (6)
Factor the left side of the equation (6). You will get
(a-9)*(a-4) = 0
with the roots a = 9 or a = 4.
Then the corresponding values of "r" are r = . (6)
Factor the left side of the equation (6). You will get
(a-9)*(a-4) = 0
with the roots a = 9 or a = 4.
Then the corresponding values of "r" are r =  = =  and r = and r =  = =  , exactly as in the answer above.
Thus the progression is {9, 6, 4} or {4, 6, 9}. , exactly as in the answer above.
Thus the progression is {9, 6, 4} or {4, 6, 9}.
|
|
|