1. Five cards are chosen from a random a standard deck of
playing cards. In how many ways can the cards be chosen
under each of the following condition.
a.) all are hearts.
13 hearts, CHOOSE 5
Answer: 13C5 = 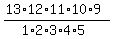 = 1287
[5 factors in the numerator, coming down from 15, 5 factors in the
denominator, coming up from 1.]
= 1287
[5 factors in the numerator, coming down from 15, 5 factors in the
denominator, coming up from 1.]
b.) Exactly three kings
Here we have two things to choose, 3 kings and 2 non-kings.
First we find the number of ways to choose 3 kings.
4 kings, choose 3. 4C3 = 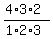 = 4
Next we find the number of ways to choose 2 non-kings.
48 non-kings, choose 2 = 48C2 =
= 4
Next we find the number of ways to choose 2 non-kings.
48 non-kings, choose 2 = 48C2 = 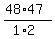 = 1128
Now for each of the 4 ways to choose the 3 kings, there
are 1128 ways to choose the 2 non-kings, so we multiply
those numbers:
4*1128 = 4512
---------------------------
= 1128
Now for each of the 4 ways to choose the 3 kings, there
are 1128 ways to choose the 2 non-kings, so we multiply
those numbers:
4*1128 = 4512
---------------------------
Use mathematical induction to prove 2+2+8+..+2^n= 2(2^n -1)
We are to prove P(n) which is
 First let's see what P(k+1) would be: [That's always the first
thing to do. Before you start an induction proof, you should
calculate P(k+1) to see where you're headed]:
To do that, replace n by k+1 in
First let's see what P(k+1) would be: [That's always the first
thing to do. Before you start an induction proof, you should
calculate P(k+1) to see where you're headed]:
To do that, replace n by k+1 in 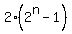 to see what P(k+1)
is, for that is what we are going for, and if we have that
beforehand, we'll know when we have arrived and the proof is
finished.
Substituting k+1 for n in
to see what P(k+1)
is, for that is what we are going for, and if we have that
beforehand, we'll know when we have arrived and the proof is
finished.
Substituting k+1 for n in 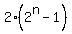 , we have
, we have
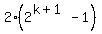 =
=  Now that we know what P(k+1) is, we know where we're going, and we'll
know we have arrived if and when we get
Now that we know what P(k+1) is, we know where we're going, and we'll
know we have arrived if and when we get  . So now we
can start the proof:
P(1): substitute n=1,
. So now we
can start the proof:
P(1): substitute n=1, 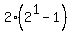 = 2, which is true, because the
first term is 2.
Assume P(k):
= 2, which is true, because the
first term is 2.
Assume P(k):  We add the next term
We add the next term 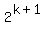 to both sides:
to both sides:


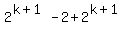

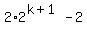

 and now we see that we get the same P(k+1) as the one that we found
in the beginning that we were going for. So the proof is finished.
So since P(1) is true, P(1) proves P(2), P(2) proves P(3), P(3)
proves P(4), etc., etc., ad infinitum.
Edwin
and now we see that we get the same P(k+1) as the one that we found
in the beginning that we were going for. So the proof is finished.
So since P(1) is true, P(1) proves P(2), P(2) proves P(3), P(3)
proves P(4), etc., etc., ad infinitum.
Edwin