.
Use mathematical induction to prove the statement is true for all positive integers n.
The integer n^3 + 2n is divisible by 3 for every positive integer n.
please show work so I can understand it:)
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
1. Let us check the statement for n = 1.
At n = 1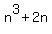 
= 
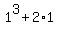= 1 + 2 = 3 is divisible by n.
So, the base of induction is valid.
2. Let us assume that the statement is true for some n = k, in other words, we assume that 
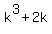is divisible by k.
We will prove that then it is true for the next integer n=k+1.
For n = k+1 we have
= 
= 
+ 
= + 
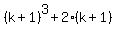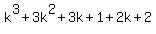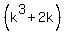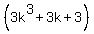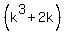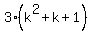. (1)
The first addend in the right side (1) is divisible by 3 due to the inductive hypothesis.
The second addend in the right side is divisible by 3, because it is multiple of 3.
Hence, the right side of (1) is divisible by 3.
Therefore, the left side, 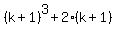is divisible by 3, too.
Thus the base of induction is proven to be valid, and the induction step is proven to be valid, too.
Due to the principle of the Mathematical induction, the statement
"for any positive integer n the number 
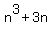is divisible by 3"
is proved.
The proof is completed.
