SOLUTION: an infinite geometric series with second term -8/9 and sum 2. what is the first term?

a*r =     (1)    This is your first equation for the second term of GP.
                     Here "a"is the first term and "r" is the common ratio of the GP.

 = 2    (2)    This is your second equation for the sum.

From the first equation express r = 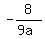 and substitute it into the second equation. You will get

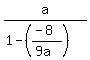 = 2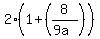,   or

 = ,   or

 = .

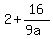Now multiply both sides by 9a. You will get

 = 18a + 16,   or 

 = .

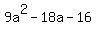Apply the quadratic formula to solve this quadratic equation. You will get

two roots  =  and  = -.

The values of "r" that correspond to these values of "a" in accordance to (1), are

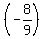 =  :  =   and   =  :  = .

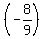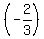The second  =  has the modulus greater than 1 and therefore generates the "divergent" geometric progression. So, the second solution doesn't fit.

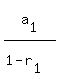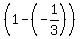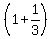Now check the equality (2) for the first solution:  =  :  =  :  =  :  = 2.  OK!

Thus there is a unique GP with the given second term and the given sum.

It is   =  ,   = .