It's easier to see when you write with larger parentheses enclosing
smaller parentheses like this:
First we remove the smallest parentheses:
Remove the medium-sized parentheses:
Remove the largest parentheses and the remaining terms will also
have positive coefficients, so we put + before the three dots:
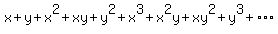Now that all terms have positive coefficients,
let's put parentheses back to separate the terms, and call it
expression (1)
(1) 
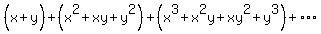Now we use the fact that 
factors as
Dividing both sides by (x-y)
Using that, expression (1) becomes:
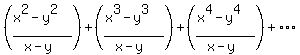And now we can conveniently write the final nth term.
Notice that the exponent in the nth term will be n+1, because the
exponent in the 1st term is 2, the exponent in the 2nd term is 3,
etc.
Factor out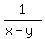 
Remove the inner parentheses:
Rearranging the terms:
Put the x terms in parentheses and write the y terms in parentheses
preceded by a - sign:
(2) 
Now we look at the sequences
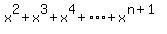and 
These are geometric series with n terms, so we use the formula
with , 
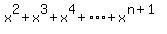and 
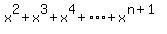
Similarly,
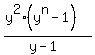Substituting those in expression (2),
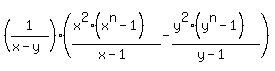I'm not going to type out all the algebra, but this can be written
Edwin
