Question 1012259: So.. for my holiday homework i was told to find a formula to sum up the tetrahedral numbers.. which are 1, 4, 10, 20, 35, 56...
And im really stuck on where to start, could you please help me step by step to sum up consecutive tetrahedral numbers? (Would appreciate if its in a easy mathematical language)
Is there any tricks to find formulas or equstions from a sequence?
Thank you :"c
Found 2 solutions by rothauserc, Edwin McCravy:
Answer by rothauserc(4718)   (Show Source): (Show Source):
You can put this solution on YOUR website! The tetrahedral numbers are found in Pascal's triangle, namely
Tn = combination of (n+2) taken 3 at a time = (n+2)! / (3! * (n+2-3)!) =
(n+2)! / (3! * (n-1)!) where Tn is the nth tetrahedral number
*****************************************************************************
another way to solve this is to note that the sum of the first n triangular numbers is the nth tetrahedral number,that is
Tn = (n(n+1)(n+2)) / 6
a triangular number can be thought of as the number of dots needed to form an equilateral triangle, namely
1, 3, 6, 10, 15, 21, and so forth
*****************************************************************************
the nth sum(Sn) of n consecutive tetrahedral numbers is
Sn = (n(n+2)(n+3)) / 24
We can derive this formula by starting with
Tn = (n(n+1)(n+2)) / 6, then expand the numerator
Tn = (n^3 + 3n^2 + 2n) / 6
Next we use the formulas for the sum of first n consecutive integers, first n squared integers and first n cubed integers, namely
Sn = (n(n+1)) / 2
Sn^2 = (n(n+1)(2n+1)) / 6
Sn^3 = (n^2(n+1)^2 / 4
Substitute these equations into our Tn formula and simplify
***************************************************************************
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website!
1, 4, 10, 20, 35, 56...
There is no one way that always works with every sequence.
But I always try a difference table first.
List the given numbers in a column:
1
4
10
20
35
56
Subtract every number from the one directly below it, and write the
result out beside each number creating a second column of numbers:
1 3
4 6
10 10
20 15
35 21
56
Do that with the second column and continue this procedure until all
the numbers in a column are the same:
1 3 3 1
4 6 4 1
10 10 5 1
20 15 6
35 21
56
Since it takes 3 columns after the first to get them all the same,
that means that a polynomial formula for the kth term must be of degree 3.
So we assume that the nth term is of the form:
 So we substitute k=1,2,3,4 and the given numbers in that and get this
system of equations:
So we substitute k=1,2,3,4 and the given numbers in that and get this
system of equations:
 which reduces to
which reduces to
 Eliminate the D's by subtracting the
1st equation from the 2nd,
2nd equation from the 3rd,
3rd equation from the 4th,
Eliminate the D's by subtracting the
1st equation from the 2nd,
2nd equation from the 3rd,
3rd equation from the 4th,
 Eliminate the C's by subtracting the
1st equation from the 2nd,
2nd equation from the 3rd,
Eliminate the C's by subtracting the
1st equation from the 2nd,
2nd equation from the 3rd,
 Eliminate the B's by subtracting the
1st equation from the 2nd:
Eliminate the B's by subtracting the
1st equation from the 2nd:

 Substitute in
Substitute in




 Substitute in
Substitute in


 Multiply through by LCD = 6 to clear the fractions
Multiply through by LCD = 6 to clear the fractions



 Substitute in
Substitute in

 Multiply through by LCD = 6 to clear the fractions
Multiply through by LCD = 6 to clear the fractions



 So the formula is:
So the formula is:
 Factor out
Factor out 
 So
So
     
    We have formulas for all three of those sums:
We have formulas for all three of those sums:


 So we now have:
So we now have:
 
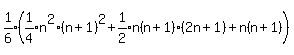  Get an LCD inside the big parentheses:
Get an LCD inside the big parentheses:
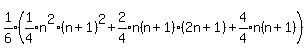  Factor
Factor  out of the big parentheses: out of the big parentheses:
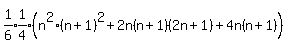  Simplify the fraction in front and factor n(n+1) out of the big
parentheses:
Simplify the fraction in front and factor n(n+1) out of the big
parentheses:
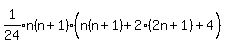  Remove the little parentheses inside the big parentheses:
Remove the little parentheses inside the big parentheses:
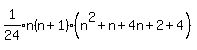  Combine terms inside:
Combine terms inside:
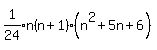  Factor the quadratic trinomial:
Factor the quadratic trinomial:
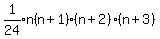 Edwin
Edwin
|
|
|