SOLUTION: The fourth term of a geometric series is 10 and the seventh term is 80. Find the common ratio, the first term and the sum of the first 20 terms( tl the nearest whole number) J

Algebra ->  Sequences-and-series -> SOLUTION: The fourth term of a geometric series is 10 and the seventh term is 80. Find the common ratio, the first term and the sum of the first 20 terms( tl the nearest whole number) J      Log On


   

Question 1012095: The fourth term of a geometric series is 10 and the seventh term is 80.
Find the common ratio, the first term and the sum of the first 20 terms( tl the nearest whole number)
James
Found 3 solutions by josgarithmetic, ValorousDawn, MathTherapy:
Answer by josgarithmetic(39617) About Me  (Show Source):
You can put this solution on YOUR website!
10%2Ar%5E3=80
r%5E3=8
r=2

Third term, 10%2Fr
Second term, 10%2Fr%5E2
First term, 10%2Fr%5E2, which is 10%2F8=5%2F4.

Look for or derive the formula for sum of any n terms.
a%28%281-r%5En%29%2F%281-r%29%29,
a is first term,
r is the common ratio,
n is the number of terms to form sum starting from first term.

Answer by ValorousDawn(53) About Me  (Show Source):
You can put this solution on YOUR website!
Remember that to find the next term, you multiply by the same number. So from the fourth term to the fifth number, you multiply by the same number as you would from the fifth to sixth. Lets call that number r.

If the fourth term is four, the fifth term is 10r. The sixth term is therefore 10r%2Ar=10r%5E2. The seventh term is 10r%5E2%2Ar=10r%5E3. But the sventh term is also 80, and thus, the two have to equal each other. We set the two equal, and solve for the common ratio r.

10r%5E3=80
r%5E3=8
r=8

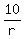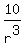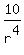We can use the same logic as before to find the first term, albeit backwards. Instead of multiplying by the number, to go backwards, you do the opposite-you divide. If the fourth term is 10, the third term is 10%2Fr, the second term is 10%2F%28r%2Ar%29=10%2Fr%5E2, the second term is 10%2Fr%5E3 and the first term is therefore 10%2Fr%5E4. We know what r is. It's 8, so we plug in and solve.

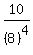
10%2F%288%29%5E4
Solved by pluggable solver: EXPLAIN simplification of an expression
Your Result:


YOUR ANSWER


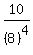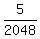  • Graphical form: 10%2F%288%29%5E4 simplifies to 5%2F2048
  • Text form: 10/(8)^4 simplifies to 5/2048
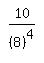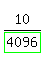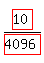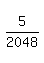
  • Cartoon (animation) form: simplify_cartoon%28+10%2F%288%29%5E4+%29
    For tutors: simplify_cartoon( 10/(8)^4 )
  • If you have a website, here's a link to this solution.

DETAILED EXPLANATION

Look at 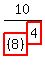10%2Fhighlight_red%28+%288%29+%29%5Ehighlight_red%28+4+%29.
Replace constants in factor: highlight_red%28+%288%29+%29,highlight_red%28+4+%29 with highlight_green%28+4096+%29
It becomes 10%2Fhighlight_green%28+4096+%29.
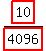Look at highlight_red%28+10+%29%2Fhighlight_red%28+4096+%29.
Factors 10 and 4096 have greatest common factor (GCF) of 2. Reducing fraction.
It becomes highlight_green%28+5+%29%2Fhighlight_green%28+2048+%29.
Result: 5%2F2048

Universal Simplifier and Solver


Done!



I will sketch out a short proof on the formula for the formula of the sum of the first n terms in a geometric series. Lets say the sum of the first n terms is equal to s. Our first term is a. Our equality will look something like this. s=a%2Bar%2Bar%5E2...ar%5En-1.. If you're wondering why the nth term has exponent n-1 rather than n, remember that you're not starting with ar, you're starting with a.

We then multiply across by r.
sr=ar%2Bar%5E2%2Bar%5E3...%2Bar%5En.
We can subtract both sides by s.
s-sr=s-ar%2Bar%5E2%2Bar%5E3...%2Bar%5En.
Remember how s=a%2Bar%2Bar%5E2...ar%5En-1.? Substitute.
s-sr=a-ar%5En
s%281-r%29=a%281-r%5En%29
s=a%2A%281-r%5En%29%2F%281-r%29.

With this formula, we plug in the numbers we want. We know the initial term a is 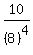10%2F%288%29%5E4, the common ratio r is 10, and the sum of terms we want to go to n is 20. s=%2810%2F%288%29%5E4%29%2A%281-%2810%29%5E20%29%2F%281-10%29

To the nearest integer, the sum of the first 20 terms, to the nearest integer, is 27126736111111111

Answer by MathTherapy(10552) About Me  (Show Source):
You can put this solution on YOUR website!

The fourth term of a geometric series is 10 and the seventh term is 80.
Find the common ratio, the first term and the sum of the first 20 terms( tl the nearest whole number)
James
1st term, or highlight_green%28a%5B1%5D+=+1.25%29

r, or common ratio = highlight_green%282%29

Sum of 1st 20 terms = 1,310,718.75 ≈ highlight_green%281310719%29