Question 1011947: What are next two terms of sequence:
-1,2,12,40,.......
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website! -1,2,12,40,.......
We find a recursion formula of the form:
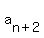  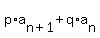 , where , where    and and    and where p and q are constants:
and where p and q are constants:
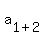  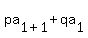
  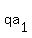
  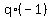
   (1)
(1)   
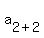  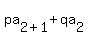

  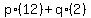
  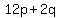 Divide through by 2
Divide through by 2
  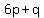 (2)
(2) 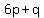   Solve the system of equations (1) and (2)
Solve the system of equations (1) and (2)
 Add the two equations:
Add the two equations:
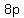  
   substitute in (1)
(1)
substitute in (1)
(1)   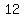  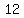  
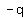  
   So the recursion formula is
So the recursion formula is
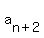  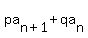 , where , where    and and    becomes
becomes
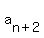  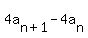 , where , where    and and    or
or
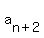  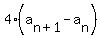 , where , where    and and    Substitute n=1 as a check
Substitute n=1 as a check
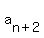  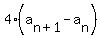
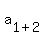  
  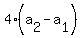
  
  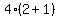
  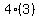
   Substitute n=2 as a check
Substitute n=2 as a check
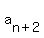  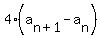
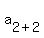  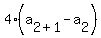
  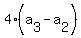
  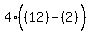
  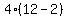
  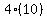
   Substitute n=3:
Substitute n=3:
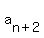  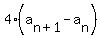
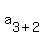  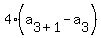
  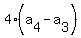
  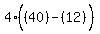
  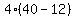
  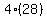
   Substitute n=4
Substitute n=4
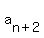  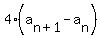
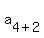  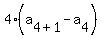
  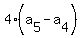
  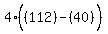
  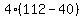
  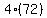
   So the sequence goes:
-1,2,12,40,112,288,704,1664,3840,8704,.......
Edwin
So the sequence goes:
-1,2,12,40,112,288,704,1664,3840,8704,.......
Edwin
|
|
|