Question 1011466: Square QRST has vertices Q(2,8),R(-4,8),S(-4,2),and T(2,2).Triangle QTU shares 2 vertices with square QRST.Whichordered pair describes point U if the area of the triangle QTU is the same as the area of square QRST?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The square has sides parallel to the x-axis,
and sides parallel to the y-axis such as 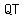 on the line on the line  . .
The length of the side of the square
is the distance
 . .
If we consider 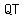 to be the base of square and triangle, to be the base of square and triangle,
the area of the square is  , ,
and the area of the triangle is
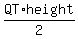 . .
We want  --> --> --> --> --> --> . .
So  is a point at a distance of is a point at a distance of  units from line units from line  containing segment base containing segment base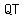 . .
It could be anywhere on line  <--> <--> , or , or
on line  --> --> . .
So without any other specification in the problem,
an infinite number of ordered pairs describe point  , ,
and an infinite number of possible triangles.
I will draw just the lines  and and  , ,
and a few of the triangles.

If we want to make triangle 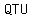 isosceles (don't we all love symmetrical shapes?), isosceles (don't we all love symmetrical shapes?),
and we want 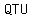 named counterclockwise, as square named counterclockwise, as square 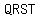 was, was,
then  is is 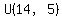 . .
|
|
|