.
Please solve:
Sn=a^2+(a+d)^2+(a+2d)^2+(a+3d)^2+....+[(a+(n-1)d]^2
Sn=a²+(a+d)²+(a+2d)²+(a+3d)²+....+[(a+(n-1)d]²
----------------------------------------------------
Let us consider one typical term 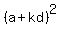 . It is
. It is
 +
+ 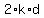 +
+ 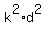 .
We need to sum up n such terms/trinomials from k = 0 to k = n-1.
By combining the first addends of these trinomials, you will get
.
We need to sum up n such terms/trinomials from k = 0 to k = n-1.
By combining the first addends of these trinomials, you will get 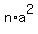 , right?
By combining the second addends of these trinomials, you will get
, right?
By combining the second addends of these trinomials, you will get 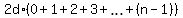 .
If you know it, this sum
.
If you know it, this sum 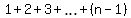 is equal to
is equal to 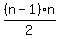 .
It is the sum of a special arithmetic progression which is the sequence of the first (n-1) natural numbers.
If you don't know it, see the lesson Arithmetic progressions in this site.
By combining the third addends of these trinomials, you will get
.
It is the sum of a special arithmetic progression which is the sequence of the first (n-1) natural numbers.
If you don't know it, see the lesson Arithmetic progressions in this site.
By combining the third addends of these trinomials, you will get 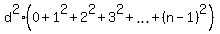 .
This sum of squares of the first (n-1) natural numbers
.
This sum of squares of the first (n-1) natural numbers 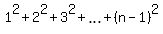 is equal to
is equal to 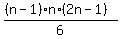 .
For the proof see, for example, the lesson Mathematical induction for sequences other than arithmetic or geometric in this site.
Now we can finalize our calculations.
.
For the proof see, for example, the lesson Mathematical induction for sequences other than arithmetic or geometric in this site.
Now we can finalize our calculations.
 =
=  =
=
=
= 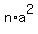 +
+ 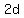 .
. +
+ 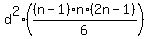 =
=
=
= 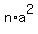 +
+ 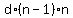 +
+  .
. .
.