Question 1000816: This is at the end of our chapter where we learned about arithmetic and geometric sequences and the binomial theorem. The question is: Expand the binomial in the difference quotient and simplify. I'm given [f(x+h)-f(x)] divided by h, I'm then given f(x)=x cubed. I don't get how this relates to series, sequences, their sums, or finding the Nth term, if you could explain the connection as well, I would appreciate it so much.
Found 2 solutions by josgarithmetic, KMST:
Answer by josgarithmetic(39618)   (Show Source): (Show Source):
You can put this solution on YOUR website! "... and the binomial theorem." You mostly need to expand that part in the difference quotient, specifically this part of the expression:
 and refer directly to the binomial theorem formula to be really formal about this. To be simpler about this, and refer directly to the binomial theorem formula to be really formal about this. To be simpler about this,  . .
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! 


I do not see how this relates to series, sequences, their sums, or finding the Nth term either.
I see how this relates to algebra in general, and polynomials in particular, and
I see how this is a sneaky introduction to derivatives,
which would belong in an early calculus lesson.
If the name of your class is pre-calculus, a sneaky introduction to derivatives may be the purpose of this problem.
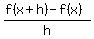 is the slope of the line AB that passes through points is the slope of the line AB that passes through points
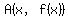 and and 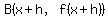 of the graph of of the graph of  . .
As you decrease 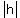 towards zero, points A and B get closer together, towards zero, points A and B get closer together,
"tending to" being the same point A, and the line AB tends to being the tangent to the curve at A.
The derivative of  is the function is the function

|
|
|