SOLUTION: Please help me solve the question if ax^3+bx^2+cx+d is divisible by ax^2+c then a,b,c,d are in ap or gp or hp or none?

Algebra ->  Sequences-and-series -> SOLUTION: Please help me solve the question if ax^3+bx^2+cx+d is divisible by ax^2+c then a,b,c,d are in ap or gp or hp or none?      Log On


   

Question 1000064: Please help me solve the question
if ax^3+bx^2+cx+d is divisible by ax^2+c then a,b,c,d are in ap or gp or hp or none?
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
In general, the answer is NONE.
Adding some requirements to the coefficients a, b, c, and d,
we could be sure to have a gp,
or even a gp that is also an ap, and a hp.

If there are no specifications about a,b,c,and d,
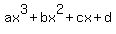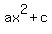ax%5E3%2Bbx%5E2%2Bcx%2Bd could be divisible by ax%5E2%2Bc if system%28a=b%2Cc=d=0%29 ,
and then a,b,c,d would be neither an ap, nor a gp, nor a hp.

If it were specified that none of the coefficients a, b,c,and d is zero,
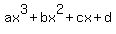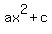when we divide ax%5E3%2Bbx%5E2%2Bcx%2Bd by ax%5E2%2Bc we find
a quotient of 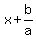x%2Bb%2Fa and
a remainder of 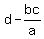d-bc%2Fa .
In that case,
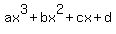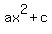if ax%5E3%2Bbx%5E2%2Bcx%2Bd is divisible by ax%5E2%2Bc , then
d-bc%2Fa=0--->d=bc%2Fa--->d%2Fb=c%2Fa .
Conversely, if d%2Fb=c%2Fa<--->d=bc%2Fa<--->ad=bc<--->d%2Fc=b%2Fa ,
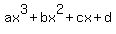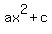then the remainder is zero, and ax%5E3%2Bbx%5E2%2Bcx%2Bd is divisible by ax%5E2%2Bc .
For d%2Fb=c%2Fa<--->d=bc%2Fa to happen,
it is not necessary that a,b,c,d form an ap, an gp, or an hp.
Sometimes a,b,c,d will be an ap, a gp, and a hp,
sometimes it will only be a gp,
but other times it will be none of those.
For example, 1,2,3,6 is neither an ap, nor a gp, nor a hp.

With d%2Fb=c%2Fa<--->d=bc%2Fa , and b=sqrt%28ac%29<--->b%2Fa=sqrt%28c%2Fa%29 ,
a,b,c,d is a gp with common ratio 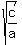sqrt%28c%2Fa%29 .
1,2,4,8 is an example.
A special case of that is when a=b=c=d , which makes a,b,c,d
a gp, an ap, and a hp.