Question 998860: The volume of a rectangular solid is 750 cubic units. The width is 7 units more than the height and the length is 1 unit more than eight times the height. Find the dimensions of the solid.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website!  = height of the rectangular solid, in linear units. = height of the rectangular solid, in linear units.
"The width is 7 units more than the height" translates as
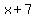 = width of the rectangular solid, in linear units. = width of the rectangular solid, in linear units.
"The length is 1 unit more than eight times the height" translates as
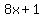 = length of the rectangular solid, in linear units. = length of the rectangular solid, in linear units.
Since the volume is the product  and equals and equals 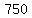 cubic units, cubic units,
 is our equation. is our equation.
It is cubic equation, and we could multiply and look for solutions whichever was we can.
However, should  be an integer, be an integer,  , , 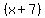 and and 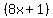 would be factors of would be factors of 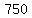 , ,
with  being the smallest of the three, and being the smallest of the three, and 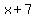 being being  units more than units more than  . .
 . .
Since the exponents of the prime factors are  , ,  , and , and  , ,
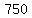 has has  factors. factors.
The smallest of them, in increasing order, are:
1, 2, 3, 5, 6, 10, 15, 25, and 30.
The only pair differing by  is is  and and  . .
If  , ,  . .

Could it be that  ? ?
If  , ,  , so , so  (in linear units, of course). (in linear units, of course).
THE CUBIC EQUATION:
Maybe you were expected to multiply and solve the resulting cubic equation.
That is a long and cumbersome process:
 --> --> --> --> --> --> --> -->
The usual way to solve  would be to find a rational solution, would be to find a rational solution,  , ,
where  is a factor of is a factor of 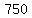 and and  is a factor of is a factor of  . .
Luckily,  with with  is a rational solution. is a rational solution.
That means that the polynomial 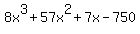 is divisible by is divisible by  . .
Dividing, we find
 <--> <--> . .
So the solutions for  are the solution for are the solution for  <--> <--> , ,
plus the solutions to  , if any. , if any.
Since  has no solutions, the only solution is has no solutions, the only solution is  . .
|
|
|