SOLUTION: the length and width of a rectangle are (3x+1) and (2x-1)cm respectively.If the area of the rectangle is 144cm,find x

Algebra ->  Rectangles -> SOLUTION: the length and width of a rectangle are (3x+1) and (2x-1)cm respectively.If the area of the rectangle is 144cm,find x       Log On


   

Question 978430: the length and width of a rectangle are (3x+1) and (2x-1)cm respectively.If the area of the rectangle is 144cm,find x
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
%283x%2B1%29+%282x-1%29=144
6x%5E2-3x%2B2x-1=144
6x%5E2-x-1=144
6x%5E2-x-1-144=0
6x%5E2-x-145=0
We need to solve the quadratic equation above.
Quadratic equations can always be solved
by "completing the square"
and by applying the quadratic formula.
Some quadratic equations can also be solved by factoring,
and 6x%5E2-x-145=0 is one of those.
To factor, we look for factors of 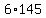6%2A145 .
No need to multiply, when we can find and recombine the prime factors:
6%2A145=%282%2A3%29%2A%285%2A29%29=%282%2A3%2A5%29%2A29=30%2A29 ,

So we can re-write 6x%5E2-x-145=0 as
%286x%2B29%29%28x-5%29=0--->system%286x%2B29=0%2C%22or%22%2Cx-5=0%29 --->system%28x=-29%2F6%2C%22or%22%2Cx=5%29 .
x=5--->system%282x-1=2%2A5-1=10-1=9%2C3x%2B1=3%2A5%2B1=15%2B1=16%29 ,
for the length and width of the rectangle to be 16 and 9cm respectively,
which makes perfect sense, so highlight%28x=5%29 is a good answer.
On the other hand,
x=-29%2F6---> ,
yielding negative numbers for the length and width of the rectangle, does not make sense.
So, x=-29%2F6 is a solution for the equation %283x%2B1%29+%282x-1%29=144 ,
but is not a solution to the word problem.