Question 970464: the perimeter of a rectangle is 100 cm. determine the possible measures of one of knowing that the area of rectangle should be minimum 500 cm
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
Let us define some variables
 = length of the rectangle, in cm. = length of the rectangle, in cm.
 = width of the rectangle, in cm. = width of the rectangle, in cm.
 =area of the rectangle in square centimeters. =area of the rectangle in square centimeters.
The way  and and  were defined, were defined,
 , and when , and when  we have that special type of rectangle that we call a square. we have that special type of rectangle that we call a square.
From geometry (and real life common sense) we know that
 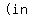  and and  . .
From the problem, we know that
  . .
From all that we know,
 ---> --->  ---> --->  ---> --->  , ,
and plugging the expression 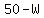 for for  in in  , ,
we get  as a function of as a function of  : :
 <---> <--->  . .
That tells us that the area of the rectangle is a quadratic function of  . .
From a memorized formula,
or from looking a the function transformed using algebra as shown below,
we realize that the function has a maximum for  , ,
when  . .
To both sides of  ,, the farther we go from ,, the farther we go from  , ,
the smaller the value for  . .
Of course, we defined  , ,  , and , and  to make sense with the "real life" situation of the problem, so they are all positive, for starters. to make sense with the "real life" situation of the problem, so they are all positive, for starters.
Also since  and and  , ,
 ---> --->  ---> --->  ---> --->  , so the function is defined for , so the function is defined for  , ,
and we get only a piece of the quadratic function,
increasing from   to a maximum for to a maximum for  , ,
when  . .
 <---> <---> <---> <---> <---> <---> 
If you need an area of 500 square centimeters, you would get it when
 , so you solve that to find the minimum width. , so you solve that to find the minimum width.
Or, you say that you want  and use the expression and use the expression
 <---> <---> to get to get
 ---> --->  ---> --->  ---> --->  (because we know that (because we know that  <---> <---> ) . ) .
Then ,

and  . .
|
|
|