SOLUTION: a rectangular sign must have an area of 11 square yards. Its length must be 6 yards more than its width.

Algebra ->  Rectangles -> SOLUTION: a rectangular sign must have an area of 11 square yards. Its length must be 6 yards more than its width.       Log On


   

Question 921208: a rectangular sign must have an area of 11 square yards. Its length must be 6 yards more than its width.
Answer by ewatrrr(24785) About Me  (Show Source):
You can put this solution on YOUR website!
 

Hi,

     .

A = Lw

(w+6)w = 11 yd^2



w^2 + 6w -11 = 0 (tossing out negative solution for unit measure)

w = 1.47213595499958,  and L = 7.47213595499958 

 


 
Solved by pluggable solver: SOLVE quadratic equation with variable


Quadratic equation ax%5E2%2Bbx%2Bc=0 (in our case 1x%5E2%2B6x%2B-11+=+0) has the following solutons:

  

  x%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

  

  For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

  

  First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%286%29%5E2-4%2A1%2A-11=80.

  

  Discriminant d=80 is greater than zero. That means that there are two solutions: +x%5B12%5D+=+%28-6%2B-sqrt%28+80+%29%29%2F2%5Ca.

  

    x%5B1%5D+=+%28-%286%29%2Bsqrt%28+80+%29%29%2F2%5C1+=+1.47213595499958

    x%5B2%5D+=+%28-%286%29-sqrt%28+80+%29%29%2F2%5C1+=+-7.47213595499958

    

    Quadratic expression 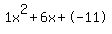1x%5E2%2B6x%2B-11 can be factored:

  1x%5E2%2B6x%2B-11+=+1%28x-1.47213595499958%29%2A%28x--7.47213595499958%29

  Again, the answer is: 1.47213595499958, -7.47213595499958.
Here's your graph:

graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+1%2Ax%5E2%2B6%2Ax%2B-11+%29