SOLUTION: The width of a rectangle is 1/4 of the length. The area is twice the perimeter. What are the dimensions of the rectangle?

Algebra ->  Rectangles -> SOLUTION: The width of a rectangle is 1/4 of the length. The area is twice the perimeter. What are the dimensions of the rectangle?      Log On


   

Question 914040: The width of a rectangle is 1/4 of the length. The area is twice the perimeter. What are the dimensions of the rectangle?
Found 2 solutions by Lenzky, MathTherapy:
Answer by Lenzky(18) About Me  (Show Source):
You can put this solution on YOUR website!
x - Length
x%2F4 - Wide
Perimeter
2x+%2B+2%28x%2F4%29+=+2x+%2B+x%2F2
Area
%28x%29%28x%2F4%29+=+x%5E2%2F4
x%5E2%2F4+=+2%282x+%2B+x%2F2%29
x%5E2%2F4+=+4x+%2B+x times both side by 4
x%5E2+=+16x+%2B+4x
x%5E2+=+20x
x%5E2+-+20x+=+0
x%28x-20%29+=+0
x+=+0&x+=+20
Checking:
Length: X+=+20
Wide: x%2F4+=+20%2F4+=+5
P= 2L + 2W
P= 2(20) + 2(5)
P= 40 + 10
P= 50
A= LW
A= 20 x 5
A= 100
2P = A
2(50) = 100
100 = 100

Answer by MathTherapy(10552) About Me  (Show Source):
You can put this solution on YOUR website!

The width of a rectangle is 1/4 of the length. The area is twice the perimeter. What are the dimensions of the rectangle?


Let width of rectangle be W

Then length = 4W

Area of rectangle: W(4W), or 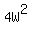4W%5E2

Perimeter of rectangle: 2(W + 4W), or 2(5W), or 10W

Therefore, we get: 4W%5E2+=+2%2810W%29

4W%5E2+=+20W

4W%5E2+-+20W+=+0

4W(W – 5) = 0

W – 5 = 0              OR          4W = 0

W, or width = highlight_green%285%29      OR           W = 0 (ignore)

Length: 4(5), or highlight_green%2820%29 units of length