Question 896654: a farmer has 120m hogwire to build a rectangular pigpen, one length of which would be along a permanent wall. The pigpen would be fenced along the three sides only. If the length is to be three times the width, what are the dimensions of the pigpen?
Found 2 solutions by josgarithmetic, MathTherapy:
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website!
a farmer has 120m hogwire to build a rectangular pigpen, one length of which would be along a permanent wall. The pigpen would be fenced along the three sides only. If the length is to be three times the width, what are the dimensions of the pigpen?
Let width be W
Then length = 3W
If width is parallel to permanent wall, then: W + 2(3W) = 120
W + 6W = 120
7W = 120
W, or width =  , or , or 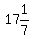 m m
Length:  , or , or  , or , or 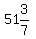 m m
If length is parallel to permanent wall, then: 2W + 3W = 120
5W = 120
W, or width = 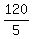 , or , or  m m
Length:  , or , or  m m
|
|
|