Question 896312: Two rectangular floors have the same area of 120cm2.if the length of one floor is 3m shorter than the other,and the widths differ by 2m,find the dimensions of each floor
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! There are meters and centimeters in your problem, and centimeters do not make sense, because a floor with a surface area of 120 square centimeters (10 cm by 12 cm for example) belongs only in a doll house.
Even if we did not want realistic measurements, if we start with a floor length that can be made 3 meters shorter, we could start with at 3.01 meters (301 cm), which would require a width of less than 1 centimeter to yield a surface area of 120 square centimeters.
There must be a typo, and the surface area of each floor is supposed to be 120 square meters.
The numbers would be ugly, and I do not think that was intended.
Here is the way to solve the reasonable problem.
The floors have a surface area of 120 square meters  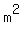 . .
 = length of the first floor in m (meters). = length of the first floor in m (meters).
 = width of the first floor in m. = width of the first floor in m.
For the first floor,
 is how we calculate its area. is how we calculate its area.
The second floor has the same surface area, but its length is less, so its width must be more.
The second floor's length measures 3 meters less, and its width measures 2 meters longer than the first floor, so
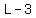 = length of the second floor in m, = length of the second floor in m,
 = width of the second floor in m, and = width of the second floor in m, and
 is the area of the second floor. is the area of the second floor.
 --> --> 
 --> -->  --> -->  --> -->  --> -->  --> --> 
 --> -->  --> --> 
We can easily solve that quadratic equation by "completing the square:
 --> -->  --> -->  --> -->  --> -->  --> -->  --> -->  . .
That would tell us that the the first floor has a width of 8 meters, and a length (in m) of
 . (Its length is 15 meters). . (Its length is 15 meters).
The second floor would be 3 meters shorter, so it is 12 meters long (15m - 3m = 12m),
and it is 2 meters wider (8m + 2m = 10 m), so it is 10 meters wide.
|
|
|