Question 882755: A rectangular piece of cardboard is 2 units longer than it is wide. From each of its corners a square piece 2 units on a side is cut out. The flaps are then turned up to form an open box that has a volume of 70 cubic units. Find the length and width of the original piece of cardboard.
Answer by josgarithmetic(39617)   (Show Source):
You can put this solution on YOUR website! x, width
x+2, length
-
2 unit square removed from each corner;
flaps then turned to meet forming box.
Base surface, 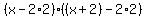 , be sure this line makes sense;
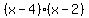
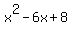
Height of this box is 2 units, so volume is  ;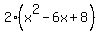
The volume was given as 70 cubic units, so  .
Simplifyable to  , and then
 ----this is FACTORABLE!
Factor the expression, pick the right (sensible) value for x, then compute x+2. Once all this, solution done.
|
|
|
