Question 832895: I can't figure out how to do this one. The volume of a rectangular box 8cm high is 120cm3. If the perimeter of the base is 20cm, find the dimensions of the box. to two decimal places.
I know volume is l x w x h which in this case = 120cm3 and if I divide what I know which is h into answer 120 = 15 Then I am left with l x w = 15cm3
I also know that a rectangle has two equal sides so the length and the width will be the same number. I just can't wrap my brain around this function
Found 2 solutions by stanbon, MathTherapy:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! The volume of a rectangular box 8cm high is 120cm3. If the perimeter of the base is 20cm, find the dimensions of the box. to two decimal places.
I know volume is l x w x h which in this case = 120cm3 and if I divide what I know which is h into answer 120/8 = 15
Then I am left with l x w = 15cm^2
----
So Length could be 3cm, then width would be 5cm.
======
All you know is that length * width = 15 cm^2.
-------
Without further information about length or width,
you can go no further.
Cheers,
Stan H.
----------------
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website! I can't figure out how to do this one. The volume of a rectangular box 8cm high is 120cm3. If the perimeter of the base is 20cm, find the dimensions of the box. to two decimal places.
I know volume is l x w x h which in this case = 120cm3 and if I divide what I know which is h into answer 120 = 15 Then I am left with l x w = 15cm3
I also know that a rectangle has two equal sides so the length and the width will be the same number. I just can't wrap my brain around this function
Let the length and width of base be L, and W, respectively
Then we can say that: 2L + 2W = 20_____2(L + W) = 2(10)_____L + W = 10_____L = 10 – W
Volume of box = LWH, or (10 – W)(W)(8) = 120



Using the quadratic equation formula,
W, or width = 8.162278 or 1.8377
Therefore, dimensions are: 8.162278 ≈  , and 1.8377 ≈ , and 1.8377 ≈ 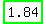
You can do the check!!
If you need a complete and detailed solution, let me know!!
Send comments, “thank-yous,” and inquiries to “D” at MathMadEzy@aol.com.
Further help is available, online or in-person, for a fee, obviously.
|
|
|