SOLUTION: Given a perimeter,P what is the largest area can you make for a quadrilateral? Express the area, A in terms of P. What kind of quadrilateral is this?

Algebra ->  Rectangles -> SOLUTION: Given a perimeter,P what is the largest area can you make for a quadrilateral? Express the area, A in terms of P. What kind of quadrilateral is this?       Log On


   

Question 773353: Given a perimeter,P what is the largest area can you make for a quadrilateral? Express the area, A in terms of P. What kind of quadrilateral is this?
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
The question should be "what is the largest area can you make for a highlight%28rectangle%29?"
It is a much more difficult geometry/trigonometry problem if you have to prove that the largest area requires the quadrilateral to have 4 right angles.
(If you had to prove that it has 4 right angles, ask again. If you do it as a thank you, I'll answer it myself).

WARNING: I write a lot of explanations, extra information and comments (added for better understanding), and alternate ways to get to solutions. What follows is not a streamlined solution in the format of your teacher's preference.

A rectangle has two parallel sides of length x, across from each other.
The other two sides, are perpendicular to the first two sides, and have length y. We do not care if x is greater, equal or less than y. It is a rectangle anyway.

The perimeter of the rectangle is calculated as
P=2%28x%2By%29
The area of the rectangle is calculated as
A=xy
system%28P=2%28x%2By%29%2CA=xy%29-->system%28P%2F2=%28x%2By%29%2CA=xy%29-->system%28y=P%2F2-x%2CA=xy%29-->system%28y=P%2F2-x%2CA=x%28P%2F2-x%29%29-->system%28y=P%2F2-x%2CA=%28P%2F2%29%2Ax-x%5E2%29
The quadratic function A=x%28P%2F2-x%29 or A=%28P%2F2%29%2Ax-x%5E2%29 has zeros at x=0 and x=P%2F2%29, and
a maximum for x=P%2F4

From x=P%2F4 on, I see two ways to get to an expression for A in terms of P.
system%28x=P%2F4%2CA=%28P%2F2%29%2Ax-x%5E2%29-->A=%28P%2F2%29%2A%28P%2F4%29-%28P%2F4%29%5E2%29-->A=P%2F8-P%2F16%29-->highlight%28A=P%2F16%29
OR
system%28x=P%2F4%2Cy=P%2F2-x%29-->system%28x=P%2F4%2Cy=P%2F2-P%2F4%29-->system%28x=P%2F4%2Cy=P%2F4%29 which means system%28x=P%2F4%2Cy=P%2F4%2CA=xy%29-->A=%28P%2F4%29%2A%28P%2F4%29-->highlight%28A=P%2F16%29
The second option also tells you that
system%28x=P%2F4%2Cy=P%2F4%29-->highlight%28x=y%29
That means that the rectangle with the greatest area is a highlight%28square%29

EXTRAS AND EXPLANATIONS:
The graph of a quadratic function is a curve called a parabola.
With A graphed along the y axis, the graph for A=%28P%2F2%29%2Ax-x%5E2%29 looks like this:
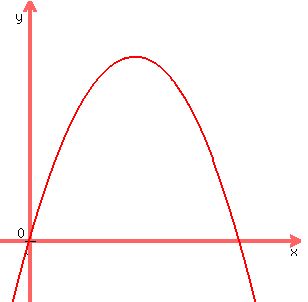graph%28300%2C300%2C-0.1%2C0.9%2C-0.2%2C0.8%2C3.5x-5x%5E2%29.
How do we know that the maximum (vertex of the parabola), and the axis of symmetry of the parabola are at x=P%2F4?
For one thing, it is obvious that A=%28P%2F2%29%2Ax-x%5E2 has zeros at x=0 and x=P%2F2%29,
and knowing that the function has a vertical axis of symmetry,
we know that x for the axis of symmetry (and the vertex/maximum that is part of that axis) has to be exactly in the middle,
at x=%28P%2F2%2B0%29%2F2=P%2F4. So I would say it's obvious.
However, if your teacher likes to see formulas, and you have to "show your work",
the axis of symmetry and maximum for quadratic function of the form f%28x%29=ax%5E2%2Bbx%2Bc or y=ax%5E2%2Bbx%2Bc
ias at x=-b%2F2a
In the case of the function A=%28P%2F2%29%2Ax-x%5E2 <--> A=-x%5E2%2B%28P%2F2%29%2Ax%2B0
a=-1, b=P%2F2, and c=0
so the axis of symmetry and maximum are at x=%28p%2F2%29%2F2 --> highlight%28x=P%2F4%29