Question 747328: What's
The length of a rectangle is 3 feet less than twice the width. The area is 44 square feet. Find the length and the width?
Answer by timvanswearingen(106)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let w be the width.
Then the length can be represented by 2w-3 (3 less than twice the width)
The area of a rectangle is given by:

Now, plug in for A, l and w.
{{44=(2w-3)(w)}}}
Distribute,

Subtract 44 from both sides:

Since I'm not sure how to show you the regrouping hourglass method on here, I've used the quadratic solver from this site to get to the solution for you. You can always use the quadratic formula when solving quadratics. See below the graph for the final explanation and answer.
| Solved by pluggable solver: SOLVE quadratic equation with variable |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:

For these solutions to exist, the discriminant  should not be a negative number. should not be a negative number.
First, we need to compute the discriminant  : :  . .
Discriminant d=361 is greater than zero. That means that there are two solutions:  . .


Quadratic expression 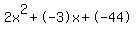 can be factored: can be factored:

Again, the answer is: 5.5, -4.
Here's your graph:
 |
Since the width cannot be a negative number, you can throw out the w=-4 solution.
Thus, the width is 5.5 feet.
The length was 3 feet less than twice the width.

Plug in 5.5 for w:

Distribute:

Simplify:

Finally, you have both. l= 8ft and w= 5.5ft
|
|
|