Question 668264: The perimeter of a rectangle is 20 ft. The length is 6ft longer than the width. Find the dimensions. Write a system of linear equations and solve the resulting system. Let x be the length and y be the width. I also need to have this information--> Write the first equation 2x+2y=? Write the second equation x=y+? What is the length and what is the width. Thanks for your help.
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website! The perimeter of a rectangle is 20 ft. The length is 6ft longer than the width. Find the dimensions. Write a system of linear equations and solve the resulting system. Let x be the length and y be the width. I also need to have this information--> Write the first equation 2x+2y=? Write the second equation x=y+? What is the length and what is the width. Thanks for your help.
Length = x; y = width
2x + 2y = 20, since twice length, plus twice width = perimeter
2(x + y) = 2(10) ----- x + y = 10 ---- eq (i)
x = y + 6, since length is 6 ft longer than width
x - y = 6 ----- eq (ii)
Elimination method:
x + y = 10 ------- eq (i)
x - y = 6 -------- eq (ii)
2x = 16 ----- Adding eqs (ii) & (i)
x, or length =  , or , or  ft ft
8 + y = 10 ---- Substituting 8 for x in eq (i)
y = 10 - 8
y, or width =  ft ft
OR
2x + 2y = 20, since twice length, plus twice width = perimeter ---- eq (i)
x = y + 6, since length is 6 ft longer than width ---- eq (ii)
Substitution method:
2(y + 6) + 2y = 20 ------- Substituting y + 6 for x in eq (i)
2y + 12 + 2y = 20
4y = 8
y, or width = 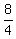 , or , or  ft ft
x = 2 + 6 ---- Substituting 2 for y in eq (ii)
x, or length =  ft ft
You can do the check!!
Send comments and “thank-yous” to “D” at MathMadEzy@aol.com
|
|
|