Question 637975: The width of a rectangle is two less than its length. If the area of the rectangle is 42, what is the length of the rectangle?
Answer by josh_jordan(263)   (Show Source): (Show Source):
You can put this solution on YOUR website! In order to solve this problem, first find the given. In this case, it tells you that the width is 2 less than the length. In other words, W=L-2. Since the question involves the area of a rectangle, we will need to use the formula for finding the area of a rectangle, which is A=L X W, where L is length and W is width. So, let's set up our two equations:
W=L - 2
42=L X W
We can substitute L - 2 for the W in the second equation. So, we would have
42 = L X (L-2) or L(L-2)
We would multiply the L-2 by L, which is L^2-2L, so we now have
42 = L^2 - 2L
When we subtract 42 from both sides of our equation, we see that we are left with a linear equation:
L^2 - 2L - 42 = 0
So, to solve for L (the length), use the quadratic formula:

which is





So, the length of our rectangle is 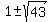
We know that the width of our rectangle 2 less than our length, so the width would be 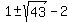 , which is , which is 
Length = 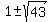
Width = 
However, neither the length nor the width of a rectangle can be a negative number. So, our length cannot be 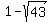 , because that is a negative number. Similarly, our width cannot be , because that is a negative number. Similarly, our width cannot be 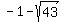 , because that too is a negative number. So, our final answer would be: , because that too is a negative number. So, our final answer would be:
Length = 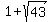
Width = 
|
|
|