Question 626824: The rectangular floor of a
shed has a length 4 feet longer than its width, and its
area is 140 square feet. Let x be the width of the floor.
(a) Write a quadratic equation whose solution gives
the width of the floor.
(b) Solve this equation.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let  be the width of the floor (in feet). be the width of the floor (in feet).
The length is 4 feet longer than the width, so it is
 (in feet). (in feet).
(a) The area in square feet can be calculated by multiplying length (in feet) times width (in feet), and it equals 140 square feet, so

That equation can be transformed into a more traditional form:
 --> -->  --> --> 
(b) The equation can be solved by factoring, or by completing the square, or by using the quadratic formula. I'll show you all 3 algebra ways of solving a quadratic equation, plus the way a fifth grader could solve the problem.
Someone who does not know algebra would not be able to write the equation, but could look for two numbers that multiply to give 140 and could be the width and length in feet. Possible products are:






The last one of those products represents the width (10 feet) times the length (14 feet, 4 more than the width) of the rectangle.
FACTORING (when it works, the easiest way):
The person who knows algebra (and became good at factoring polynomials) will do something similar, looking for integers that multiply to give the 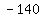 in the equation, and that will add up to the in the equation, and that will add up to the  in the equation in the equation

The integers,  and and  , are the numbers added to x in the factors of the quadratic polynomial: , are the numbers added to x in the factors of the quadratic polynomial:

The factored equation is
 with solutions that make with solutions that make  or or  : :
 and and 
The only solution to the problem is
 --> -->  (The width is 10 feet), (The width is 10 feet),
because the width in feet cannot be a negative number.
While  is a solution to is a solution to  and to the quadratic equation, it is not a solution to part (b) of the problem. and to the quadratic equation, it is not a solution to part (b) of the problem.
COMPLETING THE SQUARE:
 --> --> 
Then, adding 4 to both sides of the equal sign,
we get  on the left side. on the left side.
 --> -->  --> --> 
As  or or  , ,
 --> -->  or or 
 --> -->  --> --> 
 --> -->  , which is not a solution to the problem, because the width cannot be -14 feet. , which is not a solution to the problem, because the width cannot be -14 feet.
USING THE QUADRATIC FORMULA:
The solutions to an equation of the form  are given by are given by

In the case of equation  , ,
 , ,  , and , and 
So 



 --> -->  --> --> 
 --> -->  --> -->  , which is not a solution to the problem, because the width cannot be -14 feet. , which is not a solution to the problem, because the width cannot be -14 feet.
|
|
|