Question 581762: Suppose a farmer has 1000m of fencing to enclose a rectangular
field. What is the largest area that the farmer can enclose?
Answer by josmiceli(19441)   (Show Source): (Show Source):
You can put this solution on YOUR website! The Perimeter is:




-------------------
The Area is:



--------------------
First of all, when the coefficient of the
squared term is negative, then there is a maximum
and not a minimum.
When the equation is in the form
 , the max or min is , the max or min is
always at  , or, in this case, , or, in this case,


and I know that



The largest area that the farmer can enclose
is 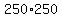 = 62,500 ft2 = 62,500 ft2
-------------------------------
I can prove this by changing the dimensions
slightly, but still keeping the same Perimeter
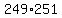 = 62,499 ft2 = 62,499 ft2
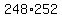 = 62,496 ft2 ( even less ) = 62,496 ft2 ( even less )
|
|
|