SOLUTION: The width of a rectangle is 4 less than twice its length. If the area of the rectangle is 183 cm^2, what is the length of the diagonal?

Algebra ->  Rectangles -> SOLUTION: The width of a rectangle is 4 less than twice its length. If the area of the rectangle is 183 cm^2, what is the length of the diagonal?       Log On


   

Question 204198: The width of a rectangle is 4 less than twice its length. If the area of the rectangle is 183 cm^2, what is the length of the diagonal?
Found 2 solutions by rfer, MathTherapy:
Answer by rfer(16322) About Me  (Show Source):
Answer by MathTherapy(10552) About Me  (Show Source):
You can put this solution on YOUR website!

Let the length of the rectangle be L
Since its width is 4 less than twice its length, then width = 2L - 4
Since its area = 183 cm^2, then we’’ll have:

L(2L – 4) = 183
2L%5E2-4L-183+=+0

Using the quadratic equation: x=%28-b%2B-sqrt%28b%5E2-4%2Aa%2Ac%29%29%2F%282%2Aa%29, where:

a = 2 ; b = - 4 ; c = - 183, we have:

L=%28--4%2B-sqrt%28-4%5E2-4%2A2%2A-183%29%29%2F%282%2A2%29

L=%284%2B-sqrt%2816%2B1464%29%29%2F%284%29

L=%284%2B-sqrt%281480%29%29%2F%284%29

L=%284%2B38.47%29%2F4 or L=%284-38.47%29%2F4

L=42.47%2F4 or L=-34.47%2F4

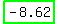
L = highlight_green%2810.62%29 or highlight_green%28-8.62%29

Since we CANNOT have a negative measurement, we reject L = - 8.62

Therefore, the length (or base) of the rectangle is 10.62 cm, and the width (or height) = 2(10.62) – 4 = 21.24 – 4 = 17.24 cm.

To now find the diagonal, we use the Pythagorean formula: a%5E2%2Bb%5E2=c%5E2, using the length and width as “a” & “b” and the diagonal as “c.”

a%5E2%2Bb%5E2=c%5E2

10.62%5E2%2B17.24%5E2=c%5E2

112.78+%2B+297.22+=+c%5E2

410=c%5E2

sqrt%28410%29=c

c, or the diagonal = highlight_green%2820.25%29 cm.