SOLUTION: A rectangular lot, whose area is 210 meter square, has one of its longer sides next to a river. The total length of fence surrounding the lot is 42 meter. Find the dimensions of

Algebra ->  Rectangles -> SOLUTION: A rectangular lot, whose area is 210 meter square, has one of its longer sides next to a river. The total length of fence surrounding the lot is 42 meter. Find the dimensions of       Log On


   

Question 159213: A rectangular lot, whose area is 210 meter square, has one of its longer sides next to a river. The total length of fence surrounding the lot is 42 meter. Find the dimensions of the lot.
Answer by vleith(2983) About Me  (Show Source):
You can put this solution on YOUR website!
Area+=+Length+%2A+Width
You are told the area is 210.
210+=+L%2AW
You are also told one side of the lot doesn't have a fence; it has a river.
The Fencing is 42.
Normally the perimeter of a rectangle is given by Perimeter+=+2%2ALength+%2B+2%2AWidth
However, in this case, one of the length sides is on the river. So, the total fencing perimeter is given by FencingPerimeter+=+1%2ALength+%2B+2%2AWidth
42+=+L+%2B+2W
42+-+2W+=+L
Substitute this value for L back into the Area equation
210+=+L%2AW
210+=+%2842-2W%29+%2A+W
210+=+-2W%5E2+%2B+42W
0+=+-2W%5E2+%2B+42W+-+210
0+=+W%5E2+-+21W+%2B+105
Use the quadratic equation to solve
Solved by pluggable solver: SOLVE quadratic equation with variable
Quadratic equation ax%5E2%2Bbx%2Bc=0 (in our case 1x%5E2%2B-21x%2B105+=+0) has the following solutons:

x%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%28-21%29%5E2-4%2A1%2A105=21.

Discriminant d=21 is greater than zero. That means that there are two solutions: +x%5B12%5D+=+%28--21%2B-sqrt%28+21+%29%29%2F2%5Ca.

x%5B1%5D+=+%28-%28-21%29%2Bsqrt%28+21+%29%29%2F2%5C1+=+12.7912878474779
x%5B2%5D+=+%28-%28-21%29-sqrt%28+21+%29%29%2F2%5C1+=+8.20871215252208

Quadratic expression 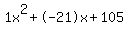1x%5E2%2B-21x%2B105 can be factored:
1x%5E2%2B-21x%2B105+=+1%28x-12.7912878474779%29%2A%28x-8.20871215252208%29
Again, the answer is: 12.7912878474779, 8.20871215252208. Here's your graph:
graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+1%2Ax%5E2%2B-21%2Ax%2B105+%29


So you have two possible answers for the width. Width is either 8.2 or 12.8
Use the Perimeter equation to find values for Length at each of these values fro width.
If width = 8.2, then 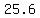Length+=+42+-+2%2A8.2 = 25.6
If width = 12.8, then 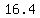Length+=+42+-+2%2A12.8 = 16.4
Since the Length in both cases is longer than the width, you lot can be either
16.4 by 12.8 or 25.6 by 8.2 meters