SOLUTION: A rectangular patio is surrounded on three sides by a fence (the remaning side is up against the house). If the area of the patio is 38 meter square, and the total length of fence

Algebra ->  Rectangles -> SOLUTION: A rectangular patio is surrounded on three sides by a fence (the remaning side is up against the house). If the area of the patio is 38 meter square, and the total length of fence       Log On


   

Question 159212: A rectangular patio is surrounded on three sides by a fence (the remaning side is up against the house). If the area of the patio is 38 meter square, and the total length of fence is 18 meters, what is the length and width of the patio.
Found 3 solutions by KnightOwlTutor, Alan3354, gonzo:
Answer by KnightOwlTutor(293) About Me  (Show Source):
You can put this solution on YOUR website!
The area of a rectangle is Length*Width
In this example X=width Y=Length
We know that the area of the rectangle is- XY=38
We know that the length of the fence that surrounds 3 sides =18
The algebraic equation for this is X+Y+X=18=2X+Y=18
We alter the perimeter equation to isolate the Y variable
2X+Y=18
Subtract 2X from both sides
Y=18-2X
Substitute 18-2X for Y in the area equation.

X(18-2X)=38
18X-2x^2=38
Rearrange terms to reflect a quadratic equation
-2x^2+18x-38=0


Solved by pluggable solver: SOLVE quadratic equation (work shown, graph etc)
Quadratic equation ax%5E2%2Bbx%2Bc=0 (in our case -2x%5E2%2B18x%2B-38+=+0) has the following solutons:

x%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%2818%29%5E2-4%2A-2%2A-38=20.

Discriminant d=20 is greater than zero. That means that there are two solutions: +x%5B12%5D+=+%28-18%2B-sqrt%28+20+%29%29%2F2%5Ca.

x%5B1%5D+=+%28-%2818%29%2Bsqrt%28+20+%29%29%2F2%5C-2+=+3.38196601125011
x%5B2%5D+=+%28-%2818%29-sqrt%28+20+%29%29%2F2%5C-2+=+5.61803398874989

Quadratic expression -2x%5E2%2B18x%2B-38 can be factored:
-2x%5E2%2B18x%2B-38+=+%28x-3.38196601125011%29%2A%28x-5.61803398874989%29
Again, the answer is: 3.38196601125011, 5.61803398874989. Here's your graph:
graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+-2%2Ax%5E2%2B18%2Ax%2B-38+%29


There are two solutions to this problems X=5.6180 and X=3.381
If we use X value of 5.6180 we can plug to find out Y value Y=18-2X
Y is 6.764 (5.6180)(6.764)=38.000152
Length of the patio is 6.764 meters and the width of the patio is 5.6180 meters

Answer by Alan3354(69443) About Me  (Show Source):
You can put this solution on YOUR website!
A rectangular patio is surrounded on three sides by a fence (the remaning side is up against the house). If the area of the patio is 38 meter square, and the total length of fence is 18 meters, what is the length and width of the patio.
---------------
A = LW = 38
F = L+2W =18 (F = total fence length)
L = 18-2W
Sub into eqn 1
W*(18-2W) = 38
18W - 2W^2 = 38
W^2 - 9W + 19 = 0
Solved by pluggable solver: SOLVE quadratic equation (work shown, graph etc)
Quadratic equation ax%5E2%2Bbx%2Bc=0 (in our case 1x%5E2%2B-9x%2B19+=+0) has the following solutons:

x%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%28-9%29%5E2-4%2A1%2A19=5.

Discriminant d=5 is greater than zero. That means that there are two solutions: +x%5B12%5D+=+%28--9%2B-sqrt%28+5+%29%29%2F2%5Ca.

x%5B1%5D+=+%28-%28-9%29%2Bsqrt%28+5+%29%29%2F2%5C1+=+5.61803398874989
x%5B2%5D+=+%28-%28-9%29-sqrt%28+5+%29%29%2F2%5C1+=+3.38196601125011

Quadratic expression 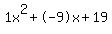1x%5E2%2B-9x%2B19 can be factored:
1x%5E2%2B-9x%2B19+=+%28x-5.61803398874989%29%2A%28x-3.38196601125011%29
Again, the answer is: 5.61803398874989, 3.38196601125011. Here's your graph:
graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+1%2Ax%5E2%2B-9%2Ax%2B19+%29

The solver uses x, so sub that for W
W = 4.5 + sqrt(5)/2
W = 4.5 - sqrt(5)/2
--------------
L = 18 - 2W
L = 18 - (9 + sqrt(5))
L = 9 - sqrt(5), W = 4.5 + sqrt(5)/2 Solution 1
------------------
L = 18 - 2W
L = 18 - (9 - sqrt(5))
L = 9 + sqrt(5), W = 4.5 - sqrt(5)/2 Solution 2
The L and W are paired as above.

Answer by gonzo(654) About Me  (Show Source):
You can put this solution on YOUR website!
it appears that the length can be any of 2 numbers and satisfy the equation.
the equation is
perimeter = l + 2*w = 18 (fence only covers 1 length)
area = l*w = 38
in the first equation, we take l = 18 - (2*w) and substitute for l in the second equation.
the second equation becomes
(18 - 2*w)*w = 38
this expands to
18*w - 2*w^2 = 38
subtracting both sides of the equation by 18*w and adding 2*w to both sides of the equation and it becomes
0 = 2*w^2 - 18*w + 38
which is the same as
2%2Aw%5E2+-+18%2Aw+%2B+38+=+0
the answer is not apparent right away so we'll use the quadratic equation to solve.
quadratic equation is w=%28%28-b%29%2Bsqrt%28b%5E2-4%2Aa%2Ac%29%29%2F%282%2Aa%29 and w=%28%28-b%29-sqrt%28b%5E2-4%2Aa%2Ac%29%29%2F%282%2Aa%29.
(-b) = +18
a = 2
c = 38
sqrt%28b%5E2-4%2Aa%2Ac%29+=+sqrt%2820%29
w+=+%2818+%2B+sqrt%2820%29%29%2F4%29 = 5.618033989
w+=+%2818+-+sqrt%2820%29%29%2F4%29 = 3.381966011
solving for l, we get
18 - 2*5.618033989 = 6.763932923
18 - 2*3.381966011 = 11.23606798
width can be 5.618033989 while length is 6.763932923, or
width can be 3.381966011 while length is 11.23606798
to prove,
perimeter = l + 2*w = 18 (fence perimeter contained only 1*l)
6.763932923 + 2*5.618033989 = 18.0000009 = 18 if the numbers weren't rounded because of the limitation of the calculator display.
also
11.23606798 + 2*3.381966011 = 18
perimeter is ok.
area = 2*l + 2*w
6.763932923 * 5.618033989 = 37.99998431 = 38 if the numbers weren't rounded because of the limitation of the calculator display.
11.23606798 * 3.381966011 = 38.00000001 = 38 if the numbers weren't rounded because of the limitation of the calculator display.
to prove that for yourself, do the calculations using a calculator and store the results without truncating and then solve again using the numbers from inside the calculator rather than the numbers in the display.