Question 1208618: The perimeter of a rectangular price tag is 28 centimeters. The area is 40 square centimeters. What are the dimensions of the price tag?
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website! .
The perimeter of a rectangular price tag is 28 centimeters. The area is 40 square centimeters.
What are the dimensions of the price tag?
~~~~~~~~~~~~~~~~~~
Let x be the length, y be the width.
Then x+y is half of the perimeter
x + y = 28/2 = 14 cm.
The average of x and y is 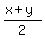 = 14/2 = 7 cm,
and we can write for the sides x and y
x = 7 + w, y = 7 - w,
where w is some unknown deviation from the average.
To find w, use the area equation xy = 40, or, which is the same
(7+w)*(7-w) = 40.
Simplify and find w
49 - w^2 = 40,
w^2 = 49 - 40 = 9,
w =  = 3.
Thus x = 7+3 = 10; y = 7-3 = 4.
ANSWER. The dimensions of the card are 10 cm (the length) and 4 cm (the width).
Solved in a simple way, closed to the mental solution.
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
Tutor @ikleyn has provided a response showing a good formal algebraic solution.
Note in particular the algebraic "trick" she used: the sum of the length and width is 14; instead of using "x" and "14-x" for the two lengths, she used "7+x" and "7-x". Doing that makes the algebra required to finish the problem easier.
Of course, if formal algebra is not required, and if the speed of reaching the solution is important -- as on a timed competitive exam -- then a quick mental solution is simple. The sum of the length and width is 14 and the product (the area) is 40, so you are looking for two numbers whose sum is 14 and whose product is 40. Two seconds of thought (if you are slow!) gives the dimensions as 4 and 10.
|
|
|
