Question 1189165: Dear Colleagues
I have the following question to find a solution to:
The length of a rectangle exceeds its breadth by 4 centimetres. If the length were halved and the breadth increased by 5 centimetres, the area would be decreased by 35 square centimetres. Find the length of the rectangle.
I do not know if I can draw in this website, but whilst trying to find the solutions, I drew 2 rectangles: the one on the left had the dimensions (x)(x+4) for width and length respectively, the one on the right had dimensions ((x+4)/2)(x+5) for length and width respectively.
The question then reads - for me - [((x+4)/2)(x+5)] - 35 = x(x+4)
Multiplying the left hand by 2 to clear the fraction, we get
[(x+4)(2x+10)]-35 = x(x+4)
and after multiplying out we get
[2x^2+10x+8x+40]-35 = x^2+4x
Collecting like terms gives us
2x^2+18x+5 = x^2+4x
which simplifies to
x^2+14x+5=0
We cannot factorise, so using the quadratic formula we get
a = 1, b= 14, c = 5
and putting all of this into the formula we get
x = (-b+/- sqrt of b^2-4ac)/2
which gives
x = (-14 +/- sqrt (14)^2-(4)(1)(5))/2
which gives us, finally, x = (-14 +/-13.23)/2
I am assuming that we need a real number for the length of the side of the rectangle, so do not wish to get into imaginary numbers...
Where have I gone wrong?
Found 4 solutions by ikleyn, Theo, greenestamps, MathTherapy:
Answer by ikleyn(52779)   (Show Source):
You can put this solution on YOUR website! .
Dear Colleagues
I have the following question to find a solution to:
The length of a rectangle exceeds its breadth by 4 centimetres. If the length were halved and the breadth
increased by 5 centimetres, the area would be decreased by 35 square centimetres. Find the length of the rectangle.
I do not know if I can draw in this website, but whilst trying to find the solutions, I drew 2 rectangles:
the one on the left had the dimensions (x)(x+4) for width and length respectively,
the one on the right had dimensions ((x+4)/2)(x+5) for length and width respectively.
The question then reads - for me - [((x+4)/2)(x+5)] - 35 = x(x+4) <<<---===
Multiplying the left hand by 2 to clear the fraction, we get
[(x+4)(2x+10)]-35 = x(x+4)
and after multiplying out we get
[2x^2+10x+8x+40]-35 = x^2+4x
Collecting like terms gives us
2x^2+18x+5 = x^2+4x
which simplifies to
x^2+14x+5=0
We cannot factorise, so using the quadratic formula we get
a = 1, b= 14, c = 5
and putting all of this into the formula we get
x = (-b+/- sqrt of b^2-4ac)/2
which gives
x = (-14 +/- sqrt (14)^2-(4)(1)(5))/2
which gives us, finally, x = (-14 +/-13.23)/2
I am assuming that we need a real number for the length of the side of the rectangle,
so do not wish to get into imaginary numbers...
Where have I gone wrong?
~~~~~~~~~~~~~~~~
Your error is in the line, which I marked by <<<---=== .
The correct form of this equation is
[((x+4)/2)(x+5)] + 35 = x(x+4).
I did not develop my solution farther, since I see that your technique is enough
in order for you complete it on your own.
Answer by Theo(13342)  (Show Source):
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
You weren't careful enough to convert the given information into an equation correctly. Your equation
[((x+4)/2)(x+5)] - 35 = x(x+4)
says that the x(x+4) is 35 less than the [((x+4)/2)(x+5)]. The given information says that the [((x+4)/2)(x+5)] is the smaller of the two expressions. ("If the length were halved and the breadth increased by 5 centimetres, the area would be decreased by 35 square centimetres").
So
[((x+4)/2)(x+5)] = x(x+4) - 35
Answer by MathTherapy(10552)  (Show Source):
You can put this solution on YOUR website!
Dear Colleagues
I have the following question to find a solution to:
The length of a rectangle exceeds its breadth by 4 centimetres. If the length were halved and the breadth increased by 5 centimetres, the area would be decreased by 35 square centimetres. Find the length of the rectangle.
I do not know if I can draw in this website, but whilst trying to find the solutions, I drew 2 rectangles: the one on the left had the dimensions (x)(x+4) for width and length respectively, the one on the right had dimensions ((x+4)/2)(x+5) for length and width respectively.
The question then reads - for me - [((x+4)/2)(x+5)] - 35 = x(x+4)
Multiplying the left hand by 2 to clear the fraction, we get
[(x+4)(2x+10)]-35 = x(x+4)
and after multiplying out we get
[2x^2+10x+8x+40]-35 = x^2+4x
Collecting like terms gives us
2x^2+18x+5 = x^2+4x
which simplifies to
x^2+14x+5=0
We cannot factorise, so using the quadratic formula we get
a = 1, b= 14, c = 5
and putting all of this into the formula we get
x = (-b+/- sqrt of b^2-4ac)/2
which gives
x = (-14 +/- sqrt (14)^2-(4)(1)(5))/2
which gives us, finally, x = (-14 +/-13.23)/2
I am assuming that we need a real number for the length of the side of the rectangle, so do not wish to get into imaginary numbers...
Where have I gone wrong?
The first error you made was forming an incorrect equation.
The easiest way to do this problem is to let the variable be what's asked for.
In other words, let the original length (requested value) be L
Then the breadth is L - 4
Halving the length gives the new length,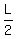 
Increasing the breadth by 5 gives the new breadth, L - 4 + 5, or L + 1
Original area: L(L - 4)
Given that the original area is reduced by 35, we get: 
 ------ Multiplying by LCD, 2
(L - 14)(L + 5) = 0
L - 14 = 0 or L + 5 = 0
Original length, or  or L = - 5 (ignore)
|
|
|
