Question 1185880: An object is thrown upward from a height of 80 ft. The initial velocity of the object is 64 ft per second. If the height h (in feet) is h=-16 +64t+80, where t is time in seconds, when will the object reach the ground?
Found 2 solutions by Alan3354, ikleyn:
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! An object is thrown upward from a height of 80 ft. The initial velocity of the object is 64 ft per second. If the height h (in feet) is h=-16 +64t+80, where t is time in seconds, when will the object reach the ground?
----------------
"If" - If the height h (in feet) is h=-16 +64t+80
==========================
It's h=-16t^2 + 64t + 80
---
-16t^2 + 64t + 80 = 0
Solve for t, ignore any negative values.
Answer by ikleyn(52925)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The problems on a projectile thrown-shot-launched vertically up are very popular.
But, as I often observed, the students who meet such problems for the first time, often write
the basic equation incorrectly, because they do not understand the meaning of its terms.
Therefore, I wrote this introductory lesson specially for beginners who don't know the subject AT ALL.
If you have the formula for a height given to you as a function of time in the form
h(t) = -at^2 + bt + c, (1)
where "a", "b" and "c" are real numbers, a > 0, then in this formula
(a) the initial height is equal to the coefficient "c" value;
(b) the initial velocity is the coefficient "b" in the formula;
(c) the coefficient "a" value is half of the gravity acceleration.
For the Earth conditions, the gravity acceleration is g = 32 ft/s^2,
if you use feet for height;
So, in this case a =  = 16 (numerical value).
(d) To find the height at the time moment "t", simply substitute the value of "t" into the formula (1) and calculate.
(e) To find the time "t" when the height has a given value h = = 16 (numerical value).
(d) To find the height at the time moment "t", simply substitute the value of "t" into the formula (1) and calculate.
(e) To find the time "t" when the height has a given value h =  , substitute h = , substitute h =  into equation (1)
and solve equation
h(t) = -at^2 + bt + c = into equation (1)
and solve equation
h(t) = -at^2 + bt + c =  . (2)
(f) To find the time when the height is maximal, use the formula . (2)
(f) To find the time when the height is maximal, use the formula
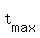 = = 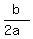 . (3)
(g) To find the maximal height, substitute the time value t= . (3)
(g) To find the maximal height, substitute the time value t= 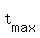 of the formula (3) into the formula (1). of the formula (3) into the formula (1).
What's all you need to know.
To see numerous examples of solved problems, look into the lessons
- Problem on a projectile moving vertically up and down
- Problem on an arrow shot vertically upward
- Problem on a ball thrown vertically up from the top of a tower
- Problem on a toy rocket launched vertically up from a tall platform
- OVERVIEW of lessons on a projectile thrown/shot/launched vertically up
in this site.
Use this file/link ALGEBRA-I - YOUR ONLINE TEXTBOOK to navigate over all topics and lessons of the online textbook ALGEBRA-I.
|
|
|