SOLUTION: A farmer has a 40 foot by 50 foot rectangular field that he wants to reduce to 10% of its original size. How wide of a strip should he cut around the edge of his field to do this?

Click here to see ALL problems on Rectangles

Question 1166193: A farmer has a 40 foot by 50 foot rectangular field that he wants to reduce to 10% of its original size. How wide of a strip should he cut around the edge of his field to do this?
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39617)   (Show Source):
You can put this solution on YOUR website!
-----the resulting area wanted

If the uniform strip to cut is x feet, then

and this to solve may be as simple as looking for the right factors of 200,... worth a try.

Or first a simplification

.
.

Answer by ikleyn(52780)   (Show Source):
You can put this solution on YOUR website!
.
A farmer has a 40 foot by 50 foot rectangular field that he wants to reduce to 10% of its original size.
How wide of a strip should he cut around the edge of his field to do this?
~~~~~~~~~~~~~~~~

            The problem formulation is OUTRAGEOUSLY inaccurate.

            The accurate formulation is THIS

A farmer has a 40 foot by 50 foot rectangular field that he wants to reduce to 10% of its original AREA. How wide of a strip should he cut around the edge of his field to do this?

The difference is in one word, but it is a KEY WORD (!)

Solution

His field is now 40 by 50 feet having the area of 40*50 = 2000 square feet. If he wants to reduce the area to 10% of its original area, then the new area should be 200 square feet. Since he wants to cut the uniform strip, the difference of new dimensions must be the same, as the difference of old dimensions, i.e. 50-40 = 10 feet. So we need to find new dimensions with the difference of 10 feet and with the product (the area) of 200. 5 seconds mental guessing give you the answer: new dimensions are 10 feet and 20 feet. And then the uniform wide of the strip is 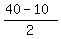= 15 feet. ANSWER

Solved.