SOLUTION: Rectangle ABCD has sides AB = 21 and AD = 28. Let P be a point inside the rectangle such that AP = 17 and BP = 10. Find the lengths PC and PD.

1.  Make a sketch.

    In the sketch, draw the perpendicular from the point P to the side AB of the rectangle.
    Let E be the foot of this perpendicular at AB.

    In the sketch, draw the perpendicular from the point P to the side AD of the rectangle.
    Let F be the foot of this perpendicular at AD.



2.  Using the Heron's formula, find the area S of the triangle APB.  It is

        area S = 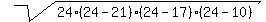 =  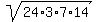= 84.

    Here in the formula  24 = 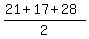  is the semi-perimeter of the triangle APB.



3.  By knowing the area of the triangle APB (84 square units) and its base AB (21 units), 
    you can find its altitude, which is 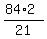 = 8 units.



4.  Now in the right angled triangle APE, you know its hypotenuse AP = 17  and one of the legs PE = 8.
    Hence, the other leg is   = 15 units.



5.  So, you know now the lengths of both perpendiculars  PE and PF, i.e. distances of the point P from 
    two sides of the rectangle.



6.  The rest of the solution is easy, and I leave it to you to complete it on your own.



ANSWER.  PD = 25; PC = 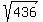 = .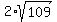