SOLUTION: a farmer with 1000 feet of fencing wants to enclose a rectangular field. Within this field he would like to make three encloures of equal areas to divide his animals. find the dime

The length will need to be spanned twice (say for the north side and south side).



The width will need to be spanned four times (for the west side, the east side, and the two dividing walls needed to make 3 enclosures).  





4W + 2L = 1000   -->  L = 500 - 2W



Now express the area in terms of L and W then substitute for L from the above equation:



Area = A = LW = (500-2W)*W = 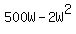  (1)



Differentiate A with respect to W:

dA/dW = 500-4W    <<< notice 2nd derivative is -4, so (1) is concave down 



 

Set to zero to find min/max (in this case max, due to concave down shape, as noted above):



  0 = 500-4W

  W = 125ft  -->  L = 250ft



Max Area = (125ft)*(250ft) =  sqft.