Question 1111020: A circle Center O touches all the sides of the regular octagon
abcdefgh shaded in the diagram the side of the octagon are of length 12cm
ba and gh are extended to meet at p
hg and ef are xtended to meet q
a)i)show that angle bah is 135 dgree ?
a)ii)show that angle aph is 90 degree ?
b)calculate
i)the length pf ph ?
ii))the length of pq ?
iii)the area of trangle aph ?
iv)the area of the octangon ?
c)calculate
i)the radius of the circle ?
ii)the area of the circle as a percentage of the area of the octagon ?
please help
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here is the circle, centered at O, and the octagon,
with sides AB, CD, EF, and GH extended in both directions
up to the point where extension meets extension:

a) Angle BAH is one of the internal angles of the octagon,
and it is the supplement of angle PAH,
which is one of the external angles of the octagon.
There is a formula about the internal angles of convex polygons,
but I find external angle measures easier to calculate.
The external angle of a convex polygon,
is the change of direction as you "turn the corner"
around one of the vertices of the polygon.
For example, as you you goo from B to A,
and turn around A to head to H,
your change of direction is angle PAH.
As you go a whole turn around any convex polygon,
your changes of direction add up to a whole turn,  , ,
so its stands to reason that for a convex polygon
the sum of the measures of the external angles is  . .
In the case of a regular octagon, like ABCDEFGH,
all  angles external have the same measure, angles external have the same measure,
so angle  . .
Angle BAH is supplementary to PAH, so
 . .
Also, in triangle PAH, as  , ,
the measure of the other angle, APH is

b) Triangle PAH is a right triangle with two congruent 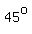 anglem anglem
and that means that the opposite sides are also congruent,
so  . .
That triangle is an isosceles right triangle,
so, according to the Pythagorean theorem
 . .
Substituting  and and  , ,




 
As ABCDEFGH is a regular octagon,
everything already prove/calculated about triangle PAH
is also true about triangles GQF, ERD , and CSB.
So,  , and as , and as  , ,
  . .
Of course, the other sides of quadrilateral PQRS also measure
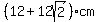 , and PQRS is a square. , and PQRS is a square.
 , ,
and each of the areas of GQF, ERD , and CSB are also 

 , so , so
  . .
c) For a regular polygon, 
The apothem of ABCDEFGH is 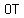 , and is the radius of the circle. , and is the radius of the circle.
 and and
 , so , so
 . .
Solving for OT, we find the radius of the circle as
  
The area of the circle is
 
The ratio of that area to the area of the octagon is
 . .
As  , ,
The area of the circle is approximately  of the area of the octagon. of the area of the octagon.
|
|
|