SOLUTION: the perimeter of a rectangular garden is 420 cm . If its length is increased by 20% and breadth is decreased by 40 % , we get the same perimeter. then the length and breadth of th

Algebra ->  Rectangles -> SOLUTION: the perimeter of a rectangular garden is 420 cm . If its length is increased by 20% and breadth is decreased by 40 % , we get the same perimeter. then the length and breadth of th      Log On


   

Question 1102530: the perimeter of a rectangular garden is 420 cm . If its length is increased by 20% and breadth is decreased by 40 % , we get the same perimeter. then the length and breadth of the new formed rectangular garden , respectively are
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39617) About Me  (Show Source):
You can put this solution on YOUR website!
system%28w%2BL=210%2Ccross%28%28w-%282%2F5%29w%29%2B%28L%2B%282%2F5%29L%29=210%29%29

System should be system%28w%2BL=210%2C%28w-%282%2F5%29w%29%2B%28L%2B%281%2F5%29L%29=210%29

-

3w%2F5%2B6L%2F5=210
3w%2B6L=1050
3%28210-L%29%2B6L=1050
630-3L%2B6L=1050
3L=1050-630
L=140andw=70, originaldimensions



--------The following work and results are wrong-----------
%283%2F5%29w%2B%287%2F5%29L=210
3w%2B7L=1050
3%28210-L%29%2B7L=1050
630-3L%2B7L=1050
4L=1050-630
4L=420
cross%28L=105%29------------length of the ORIGINAL garden
-
cross%28w=105%29-----------width of the ORIGINAL garden
Question asks for the new garden; not for the original garden.
NEW garden dimensions:
cross%28126=L%2A1.20%29
-
cross%2863=w%2A0.60%29

Answer by ikleyn(52785) About Me  (Show Source):
You can put this solution on YOUR website!
.
the perimeter of a rectangular garden is 420 cm . If its length is increased by 20% and breadth is decreased by 40 % ,
we get the same perimeter. then the length and breadth of the new formed rectangular garden , respectively are
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

        -----------------------------------------------------------------------------------------------
        The solution by @josgarithmetic is not correct. The correct solution is placed below.
        ----------------------------------------------------------------------------------------------- 


Let L be the length and W be the width of the rectangular garden (the original dimensions).


Then the first equation is

2L + 2W = 420,   or  L + W = 210.


The second equation is 

2*(1.2L) + 2*(0.6W) = 420,   or  1.2L + 0.6W = 210.


So, you have the system of 2 equations in 2 unknowns

   L +    W = 210,    (1)
1.2L + 0.6W = 210.    (2)


From eq(1) express W = 210-L  and substitute it into eq(2). You will get

1.2L + 0.6*(210-L) = 210,

1.2L + 0.6*210 - 0.6L = 210  ====>  0.6L = 210 - 0.6*210 = 0.4*210  ====>  L = 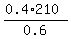%280.4%2A210%29%2F0.6 = 140.


Thus we just found L = 140 cm.


Then W = 210 - L = 210 - 140 = 70 cm.


The original length was 140 cm.  The original width was 70 cm.


Check.   140 + 70 + 140 + 70 = 420.    ! Correct !

         2*140*1.2 + 2*70*0.6 = 420.   ! Correct !


The new dimensions are:  1.2*L = 1.2*140 = 168 cm (length)  and  0.6*W = 0.6*70 = 42 cm.


Answer.  The new dimensions are:  168 cm (length)  and  42 cm (width).

Solved.