Question 1102143: An open box is formed from a rectangular piece of cardboard that is 3 in. longer than it is wide, by removing squares of side 2 in. from each corner and folding up the sides. If the volume of the carton is then 216 in^3, what were the dimensions of the original piece of cardboard?
Found 3 solutions by stanbon, ikleyn, richwmiller:
Answer by stanbon(75887)   (Show Source):
You can put this solution on YOUR website! An open box is formed from a rectangular piece of cardboard that is 3 in. longer than it is wide, by removing squares of side 2 in. from each corner and folding up the sides. If the volume of the carton is then 216 in^3, what were the dimensions of the original piece of cardboard?
-----
Original dimensions of the rectangular piece::
width = w inches
length = w+3 inches
-------------------------
After cutting out the 2 by 2 squares the remaining width and length dimensions are:
new width :: w-4 inches
new length:: w+3-4 = w-1 inches
------------------
Volume = length * width * height
216 = (w-1)*(w-4)*w
216 = (w^2-5w+4)*w
w^3 - 5w^2 + 4w - 216 = 0
---------------------------
w = 7.93 (original width)
w+3 = 10.93 (original length)
-------------
Cheers,
Stan H.
-----------------
-------
Answer by ikleyn(52786)  (Show Source):
You can put this solution on YOUR website! .
The area of the bottom of the box is its volume 216 in^3 divided by the height 2 in:
area = 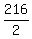 = 108 square inches.
It is clear that the dimensions of the box are 2+2 = 4 inches less than the dimensions of the original piece of cardboard.
Also, it is clear that the difference of dimensions of the bottom of the box is the same as for the original cardboard, i.e. 3 inches.
So, you need to find two integer numbers that differ in 3 units and multiply up to 108.
This numbers are 9 and 12.
Thus the bottom of the box has the dimensions of 9 in and 12 in.
Then the original cardboard has dimensions 9+4 = 13 inches and 12+4 = 16 inches.
Answer by richwmiller(17219)  (Show Source):
You can put this solution on YOUR website! continuing Stan's work before he erred.
Volume = length * width * height
216 = (w-1)*(w-4)*w
height =2
216 = (w-1)*(w-4)*2
108=(w-1)*(w-4)
108=w^2-5w+4
0=w^2-5w-104
factor
(w+8)*(w-13)=0
Taking only the positive solution
original w=13 inches
cardboard that is 3 in. longer than it is wide
original length=w+3=16 inches
|
|
|
