SOLUTION: the length of a rectangle is 18 cm more than the width. A second rectangle is 6cm shorter and 3cm wider than the first and has a perimeter of 126cm. find the dimensions of each rec

Let L and W are the length and the width of the first rectangle ( in centimeters).

Then from the condition, you have this equation 

L - W = 18.       (1)


The second rectangle has the dimensions (L-6) and (W+3), according to the condition.

Hence, its perimeter is  2*(L-6) + 2*(W+3), and you have the second equation

2*(L-6) + 2*(W+3) = 126,    or, equivalently,   L-6 + W+3 = 63,  or, equivalently,

L + W = 66.       (2)


Thus from the condition you have the system of two equations (1) and (2). To solve it, add the equations. You will get

2L = 18 + 66 = 84  ====>  L = 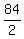 = 42.


Thus the length of the first rectangle is 42 cm.

Then its width is  42-18 = 24 cm.


The dimension of the other rectangle are 42-6 = 36 cm  and  24+3 = 27 cm.