Question 1006745: Prove that quadrilateral PLUS with vertices P(2,1), L(6,3), U(5,5), and S(1,3) is a rectangle but not a square
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website! Prove that quadrilateral  with vertices P( with vertices P( , , ), L( ), L( , , ), U( ), U( , , ), and S( ), and S( , , ) is a rectangle but not a square ) is a rectangle but not a square
by definition,a rectangle is a quadrilateral that has opposite sides are parallel and of equal length
so, we need to find the distance between vertices which is the length of the sides
if the distance between points  and and  is same as the distance between points is same as the distance between points  and and  , then the length of the sides , then the length of the sides 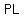 and and  are same, or are same, or 
and if the distance between points  and and  is same as the distance between points is same as the distance between points  and and  , then the length of the sides , then the length of the sides 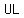 and and 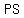 are same, or are same, or 
finally, if  and and 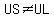 then a quadrilateral is a rectangle then a quadrilateral is a rectangle
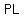
and 
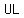
and
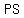
as you can see,  and and  ;so, a quadrilateral is a rectangle ;so, a quadrilateral is a rectangle

|
|
|