SOLUTION: A gardner ordered 60 square slabs measuring 1m by 1m. List different rectangular arrangements? and Find its perimeter and area? I have tried solving it. Kindly help is it correct?

Algebra ->  Rectangles -> SOLUTION: A gardner ordered 60 square slabs measuring 1m by 1m. List different rectangular arrangements? and Find its perimeter and area? I have tried solving it. Kindly help is it correct?      Log On


   

Question 1003630: A gardner ordered 60 square slabs measuring 1m by 1m. List different rectangular arrangements? and Find its perimeter and area?
I have tried solving it. Kindly help is it correct?
1) 12m long and 5m wide, Perimeter=34m and Area= 60 m-square
2) 20 m long and 3 m wide, Perimeter= 64m and Area= 60 m-square
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
Those are two of the many possible arrangements, and you correctly calculated the perimeter.
Th area is 60 square meters for all arrangements of course,
because the gardener is laying down 60 slabs, each with a 1 square meter surface area.

To find them all, we must list them systematically.
The width and length of the rectangle (in meters or number of slabs) must divide 60 evenly.
So 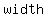width and length {would be factors of 60 such that
width%2Alength=60<-->length=60%2Fwidth .
We look for small factors of 60 that could be the width, and we fond the corresponding length.
We try 1, 2, 3, etc, in order, and see if each one is a factor.
It could be:
width=1 , and length=60%2F1=60 ,
width=2 , and length=60%2F2=30 ,
width=3 , and length=60%2F3=20 ,
width=4 , and length=60%2F4=15 ,
width=5 , and length=60%2F5=12 ,
width=6 , and length=60%2F6=10 .
So we found 6 different ways to arrange those 60 slabs in a rectangle.
7 , 8 , and 9 are not factors (they do not divide 60 evenly).
10 is a factor, but we cannot say that width=10 ,
because we had already found a rectangle with width=6 , and length=10 above,
and since the side measuring 10 was the longest side,
it is a length not a width.