SOLUTION: (a) Graph the function f(x)= x^3 - 4 (b) Approximate to the nearest tenth, the real root of the equation f(x)= x^3 - 4 = 0 please help me

Algebra ->  Rational-functions -> SOLUTION: (a) Graph the function f(x)= x^3 - 4 (b) Approximate to the nearest tenth, the real root of the equation f(x)= x^3 - 4 = 0 please help me       Log On


   

Question 92199This question is from textbook Algebra and Trigonometry
: (a) Graph the function f(x)= x^3 - 4
(b) Approximate to the nearest tenth, the real root of the equation
f(x)= x^3 - 4 = 0 please help me This question is from textbook Algebra and Trigonometry

Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
a) "Graph the function f(x)= x^3 - 4"


In order to graph y=x%5E3-4, we need to plot some points.
We can start at any x value, so lets start at x=-2



Lets evaluate 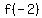f%28-2%29

f%28x%29=x%5E3-4 Start with the given polynomial


f%28-2%29=%28-2%29%5E3-4 Plug in x=-2


f%28-2%29=%28-8%29-4 Raise -2 to the third power to get -8


f%28-2%29=-12 Now combine like terms


So when x=-2, f%28-2%29=-12


So our 1st point is (-2,-12)



----Now lets find another point----



Lets evaluate 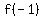f%28-1%29

f%28x%29=x%5E3-4 Start with the given polynomial


f%28-1%29=%28-1%29%5E3-4 Plug in x=-1


f%28-1%29=%28-1%29-4 Raise -1 to the third power to get -1


f%28-1%29=-5 Now combine like terms


So when x=-1, f%28-1%29=-5


So our 2nd point is (-1,-5)



----Now lets find another point----



Lets evaluate f%280%29

f%28x%29=x%5E3-4 Start with the given polynomial


f%280%29=%280%29%5E3-4 Plug in x=0


f%280%29=%280%29-4 Raise 0 to the third power to get 0


f%280%29=4 Remove any zero terms


So when x=0, f%280%29=-4


So our 3rd point is (0,-4)



----Now lets find another point----



Lets evaluate f%281%29

f%28x%29=x%5E3-4 Start with the given polynomial


f%281%29=%281%29%5E3-4 Plug in x=1


f%281%29=%281%29-4 Raise 1 to the third power to get 1


f%281%29=-3 Now combine like terms


So when x=1, f%281%29=-3


So our 4th point is (1,-3)



----Now lets find another point----



Lets evaluate f%282%29

f%28x%29=x%5E3-4 Start with the given polynomial


f%282%29=%282%29%5E3-4 Plug in x=2


f%282%29=%288%29-4 Raise 2 to the third power to get 8


f%282%29=4 Now combine like terms


So when x=2, f%282%29=4


So our 5th point is (2,4)


Now lets make a table of the values we have calculated 



 xy



 -2-12
 

 -1-5
 

 0-4
 

 1-3
 

 24
Now plot the points



Now connect the points to graph y=x%5E3-4 (note: the more points you plot, the easier it is to draw the graph)




b)
"approximate to the nearest tenth, the real root of the equation
f(x)= x^3 - 4 = 0 "


x%5E3+-+4+=+0

x%5E3+=+4 add 4 to both sides

x+=+root%283%2C4%29 Take the cube root of both sides

So the solution is approximately 1.5874010519682 which rounds to 1.6